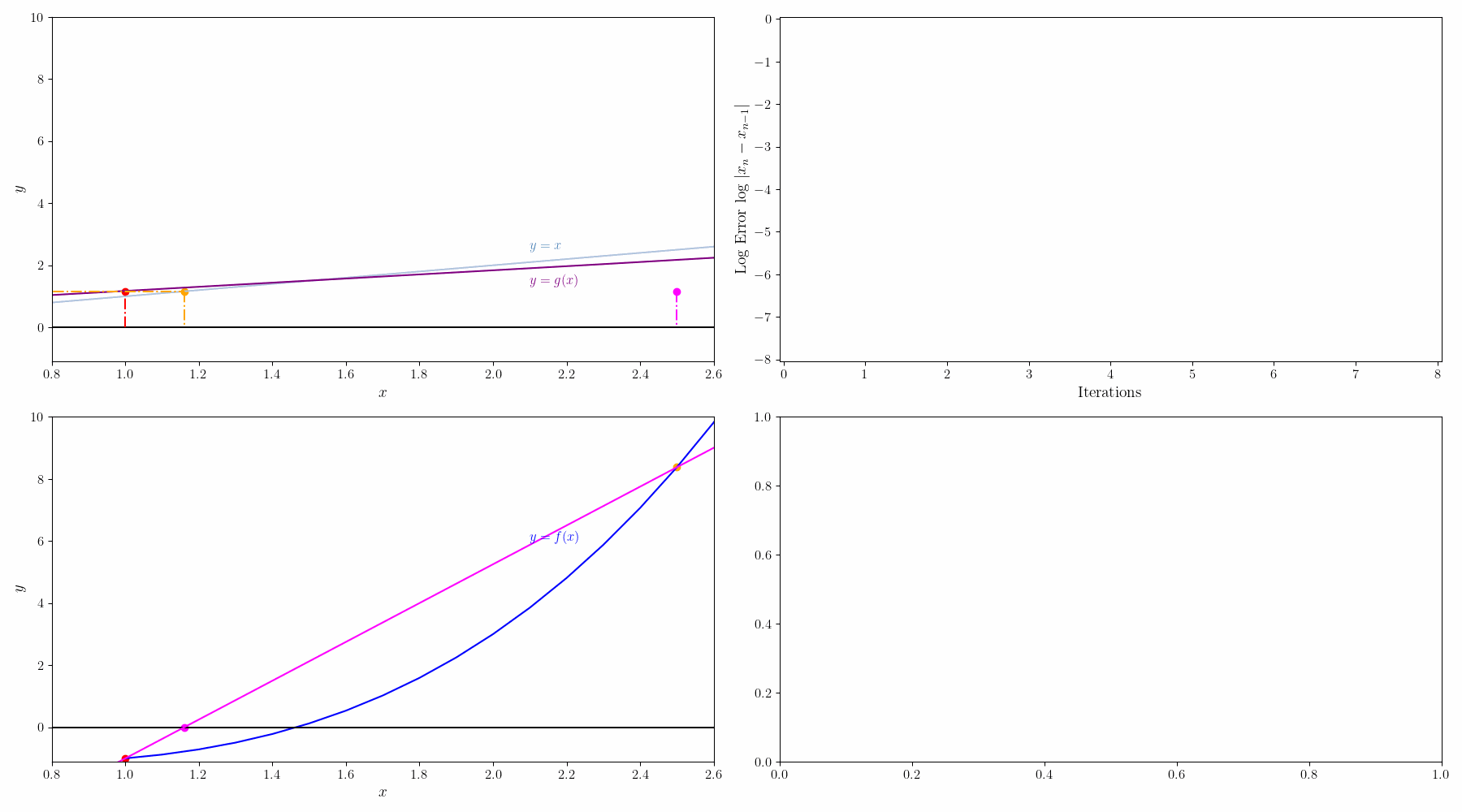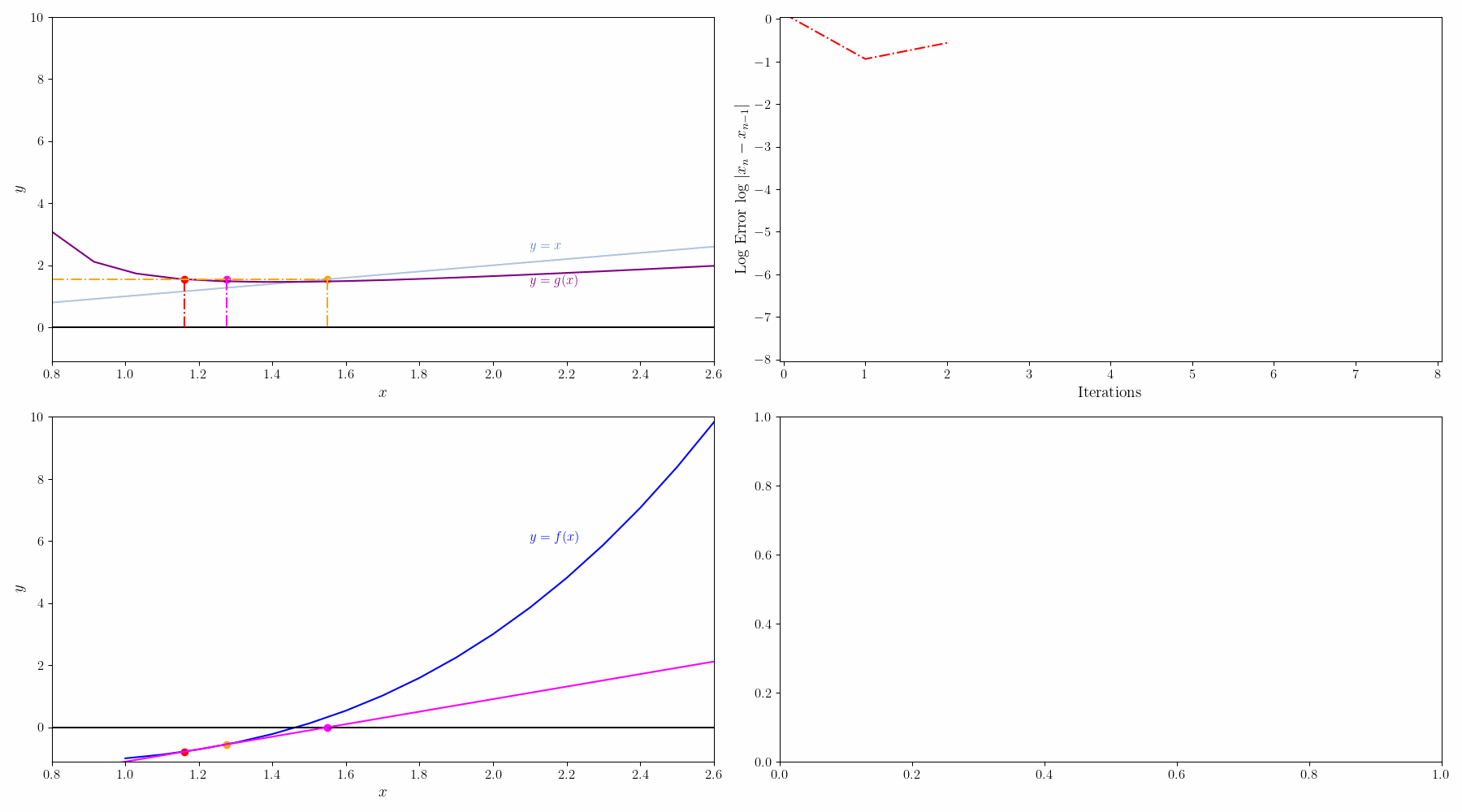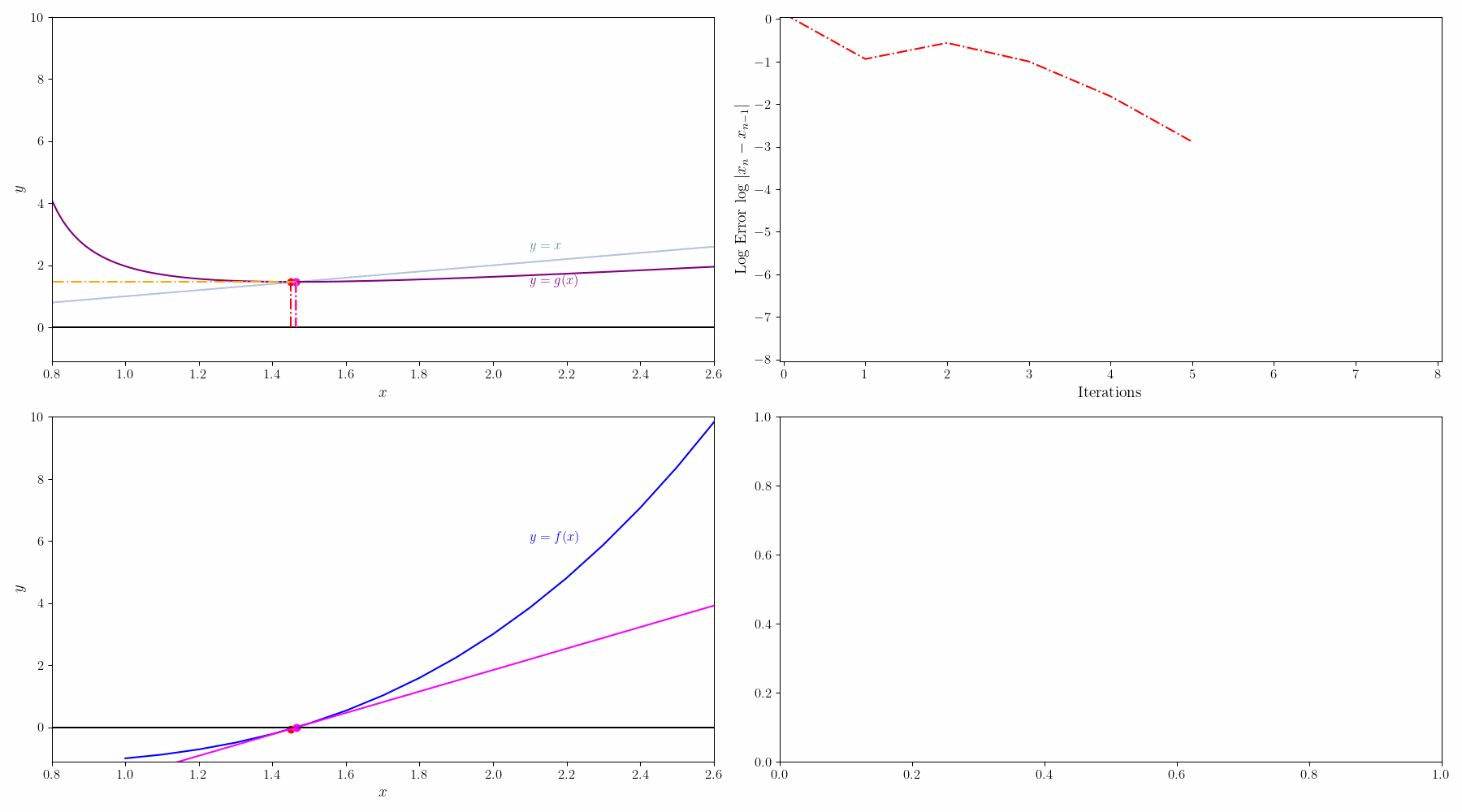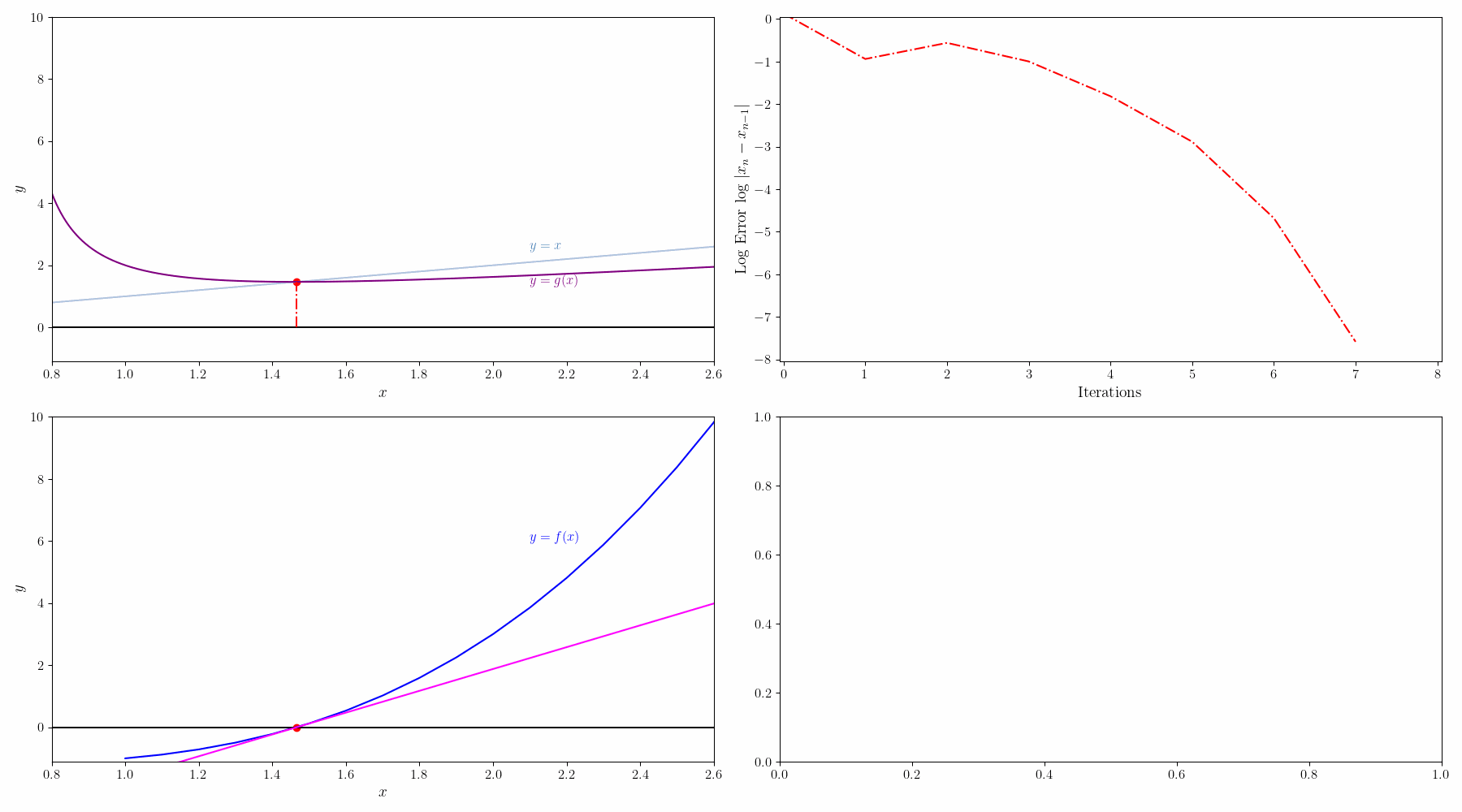Root finding methods (방정식의 근)

Jan 3, 2023 · 3 min read ·

구간법 (Braketing method)

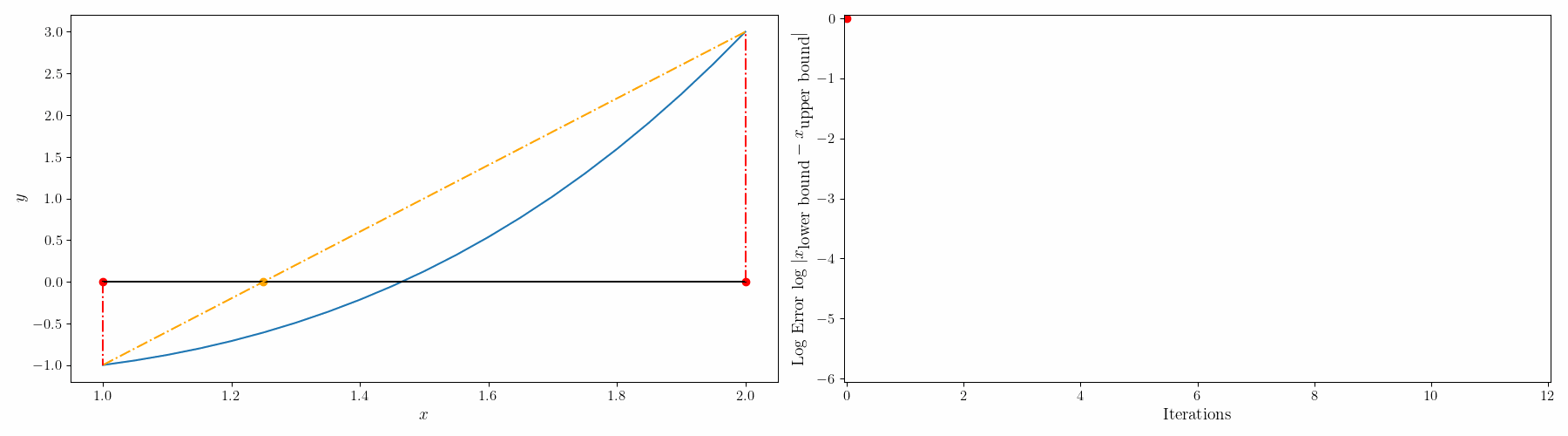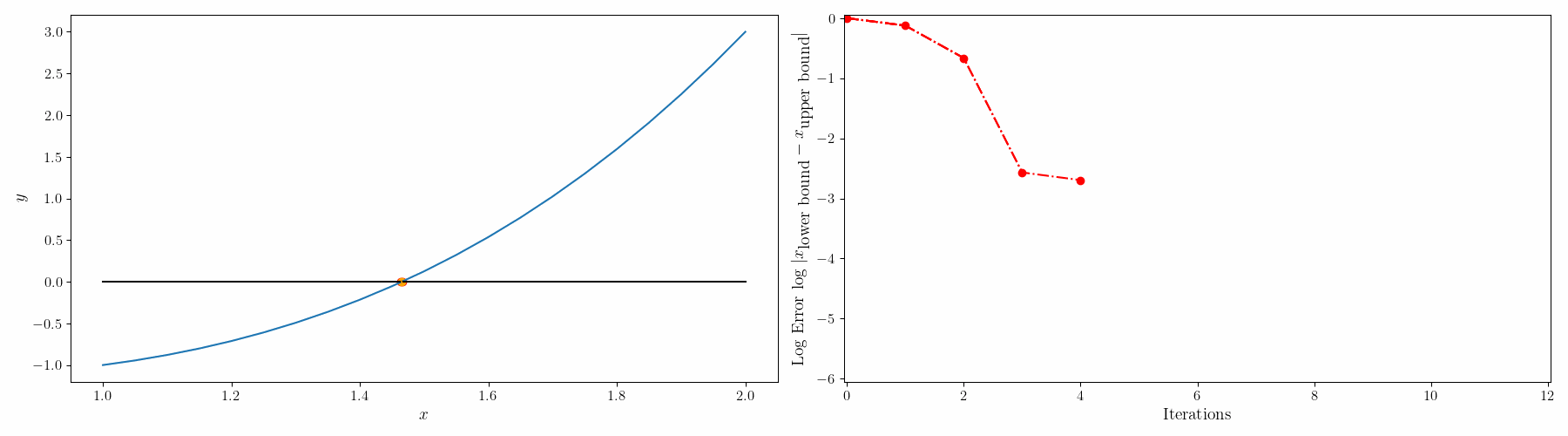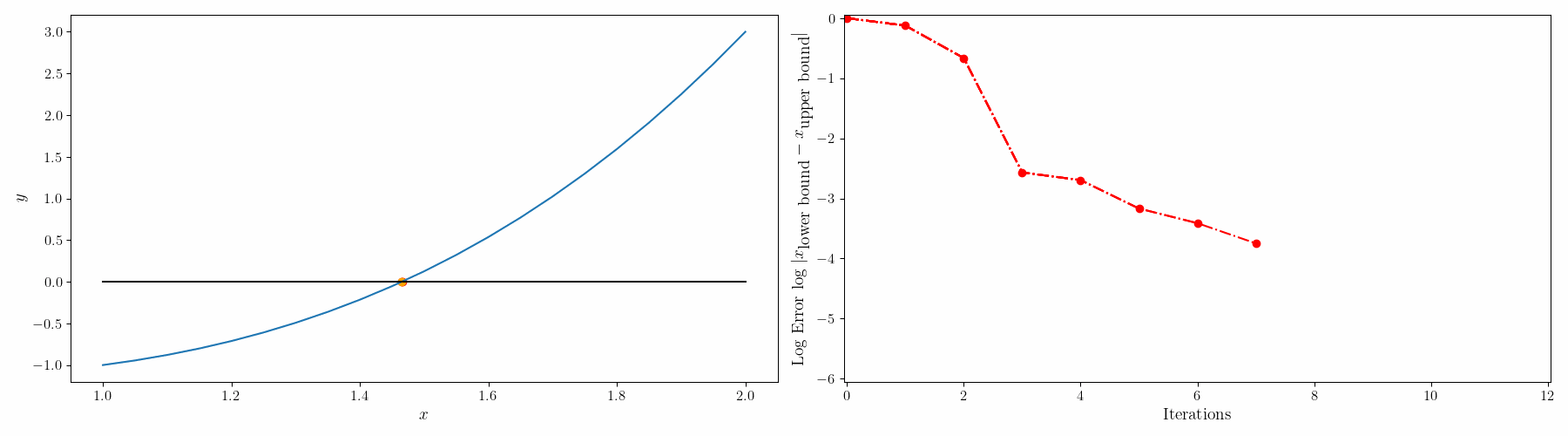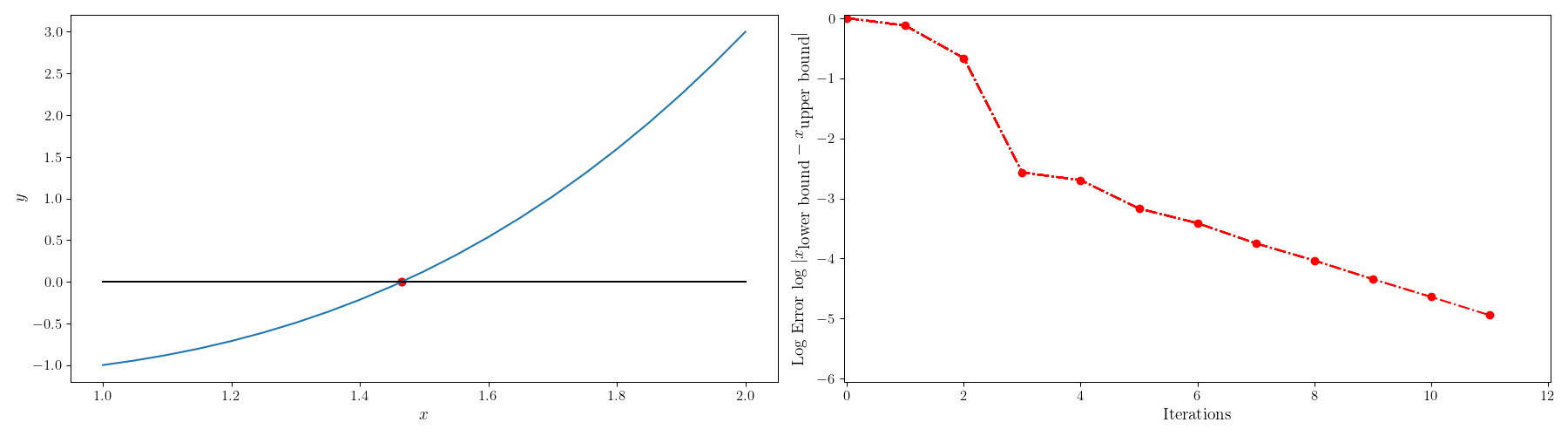
연속함수 $f(x)$ 의 값이 구간의 양 끝 $a \leq x \leq b$ 에서 조건 $f(a)f(b)<0$ $[f(a)$의 값과 $f(b)$의 값의 부호가 서로 다르다$]$을 만족하면 구간 내부에 $f(x)=0$을 만족하는 $x$가 적어도 한 개가 존재한다. 이렇게 근이 존재하는 구간을 알 때는 이분법(bisection), 가위치법(False-position method), 수정가위치법(modified false-position method) 과 같은 구간법을 적용해서 방정식의 근(해)를 구할 수 있다.

Bisection method (이분법)

$c = \frac{a+b}{2},\quad a < c < b$ 를 만족하는 $c$ 를 찾는다.
$f(c)$를 검사하여 $f(c)\leq \epsilon, \quad \epsilon=10^{-6}$를 확인한다.
만족하지 않으면 $a = c$ when $f(c)f(b)<0$ 또는 $b = c$ when $f(a)f(c)<0$
1을 반복한다.

장점: 허용오차가 주어질 경우, 해가 존재한다고 알려진 구간에서 허용오차 내의 해를 찾기 위해 연산을 반복해야하는 횟수를 알 수 있다. $$n=\log_{2}\frac{|a-b|}{\epsilon} \quad \text{from} \quad \epsilon = \frac{|a-b|}{2^n}$$ 비해석함수에도 사용할 수 있다.

단점: 문제에 따라서 시간이 많이 걸릴 수 있다. 다중근을 가지는 함수의 경우에 어떤 근이 구해질 수 알 수 없다.

False-position method (가위치법)

이분법과 비슷하지만 이분법보다 빠르게 수렴한다. 이분법은 $f(x)$ 값을 고려하지 않지만 가위치법은 $f(x)$ 값을 이용해서 다음 구간을 정한다.

$c = b-f(b)\frac{b-a}{f(b)-f(a)},\quad a < c < b$ 를 만족하는 $c$ 를 찾는다.
$f(c)$를 검사하여 $f(c)\leq \epsilon, \quad \epsilon=10^{-6}$를 확인한다.
만족하지 않으면 $a = c$ when $f(c)f(b)<0$ 또는 $b = c$ when $f(a)f(c)<0$
1을 반복한다.

단점: 그래프가 선형직선이랑 유사할 경우 해의 수렴이 늦어진다. (Stagnation point가 생겨서 인건가... 여튼, stagnation point라고 bound 하나가 한 지점에 fix 되어 있으면 수렴이 늦어짐

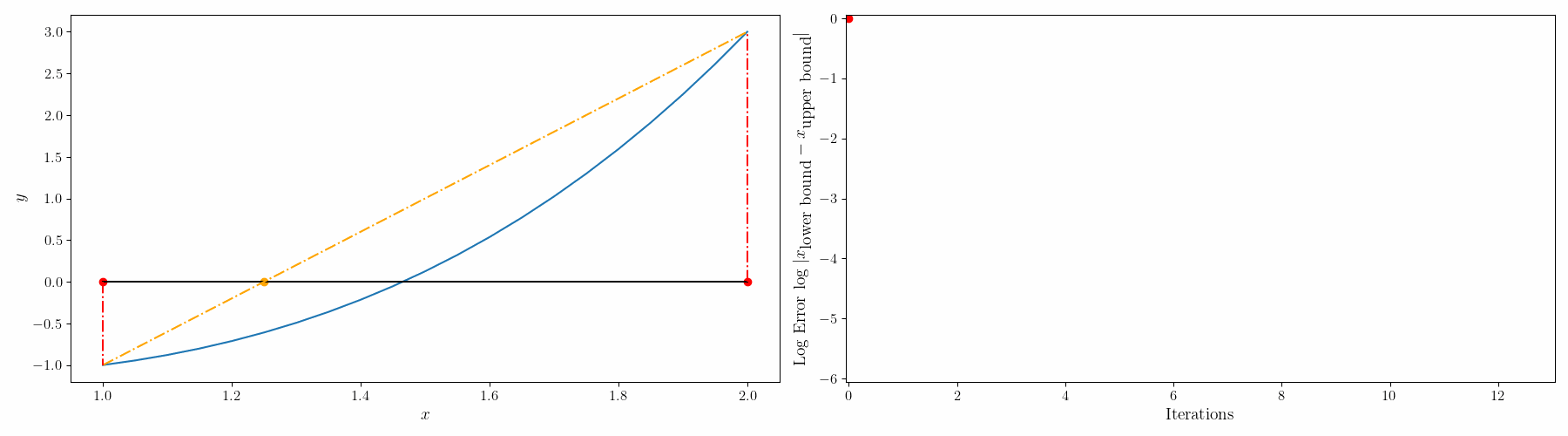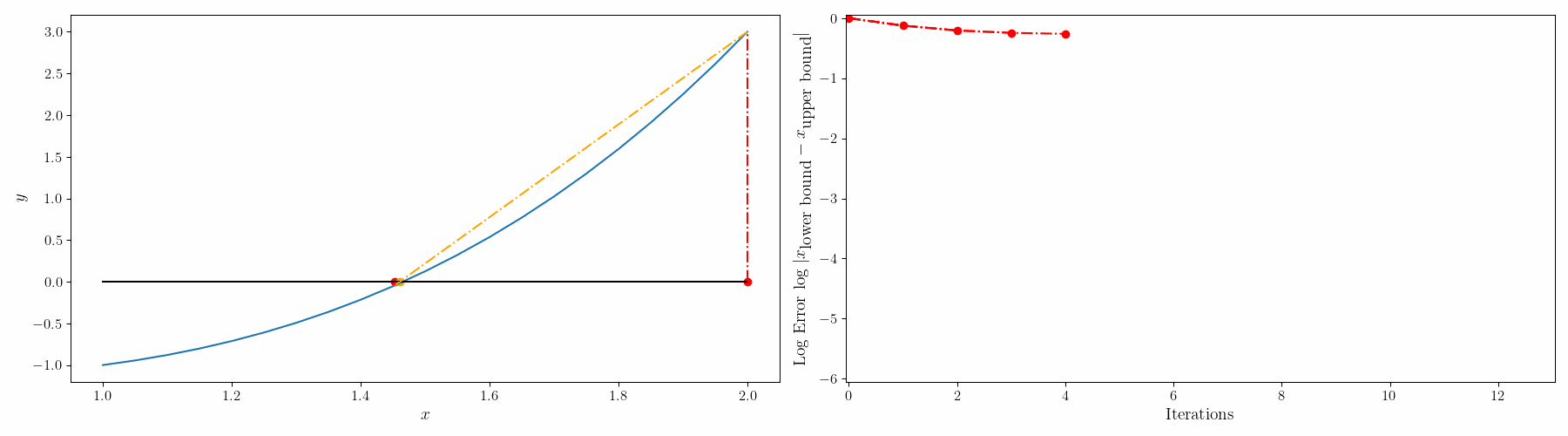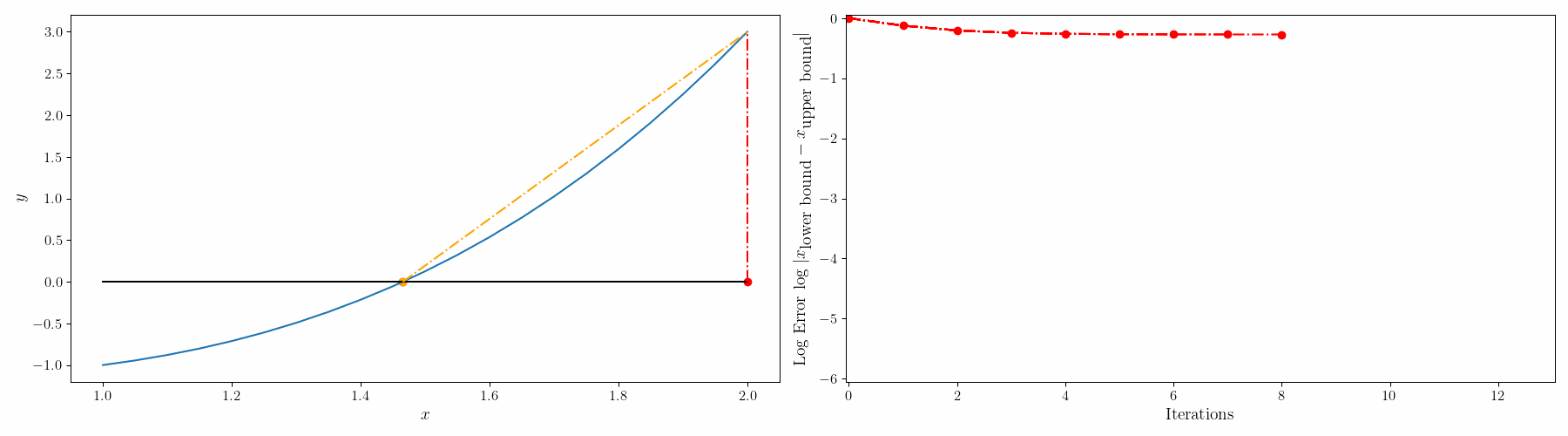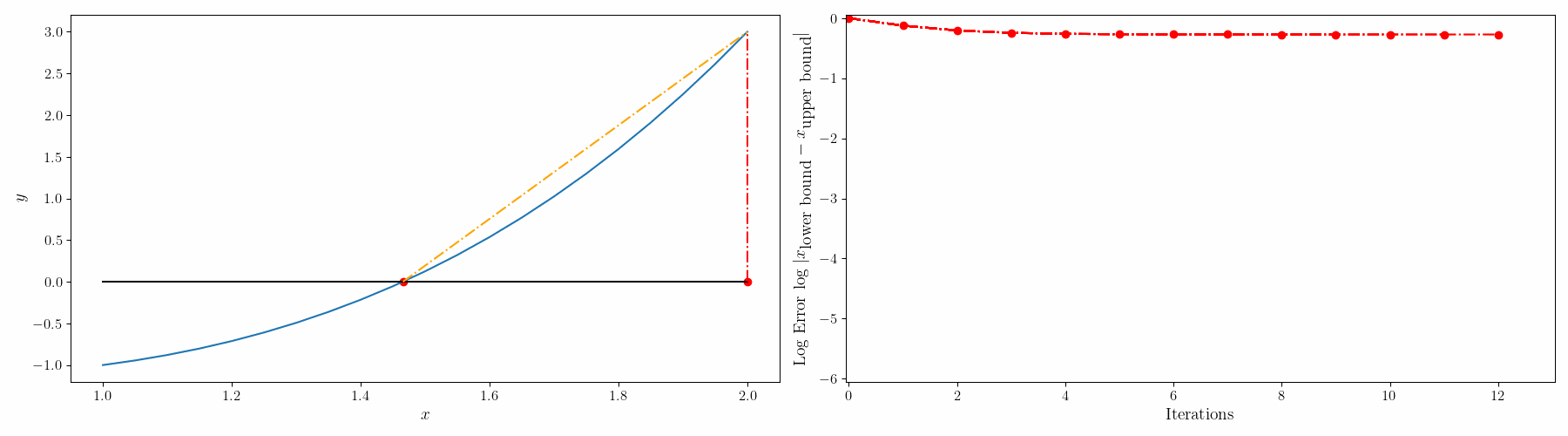
이를 개선하기 위해서 modified false-position method(수정가위치법)를 사용할 수 있다.

수정가위치법은 강제로 이 stagnation point를 움직여준다. 위의 가위치법 1번 절차를 아래의 절차로 바꿔주면 됨.

$c = b-f(b)\frac{b-a}{f(b)- \mathbf{f(a)/2} },\quad a < c < b$ 를 만족하는 $c$ 를 찾는다.

또는

$c = b-\mathbf{f(b)/2}\frac{b-a}{\mathbf{f(b)/2}-f(a) },\quad a < c < b$ 를 만족하는 $c$ 를 찾는다.

개방법 (open method)

개방법은 구간법과는 다르게 근이 존재하는 구간을 알지 못해도 되고 초기값에서 선택해서 시작한다. 이 초기값 선정에 의해서 근이 수렴 속도가 달라지지만 보통 구간법보다는 빠르게 수렴한다는 장점이 있다. 하지만 근을 찾을 수 있다는 것이 보장되지 않는다. 개방법에는 고정점 반복법, 뉴턴법, 할선법이 있다.

Fixed point method (고정점 반복법)

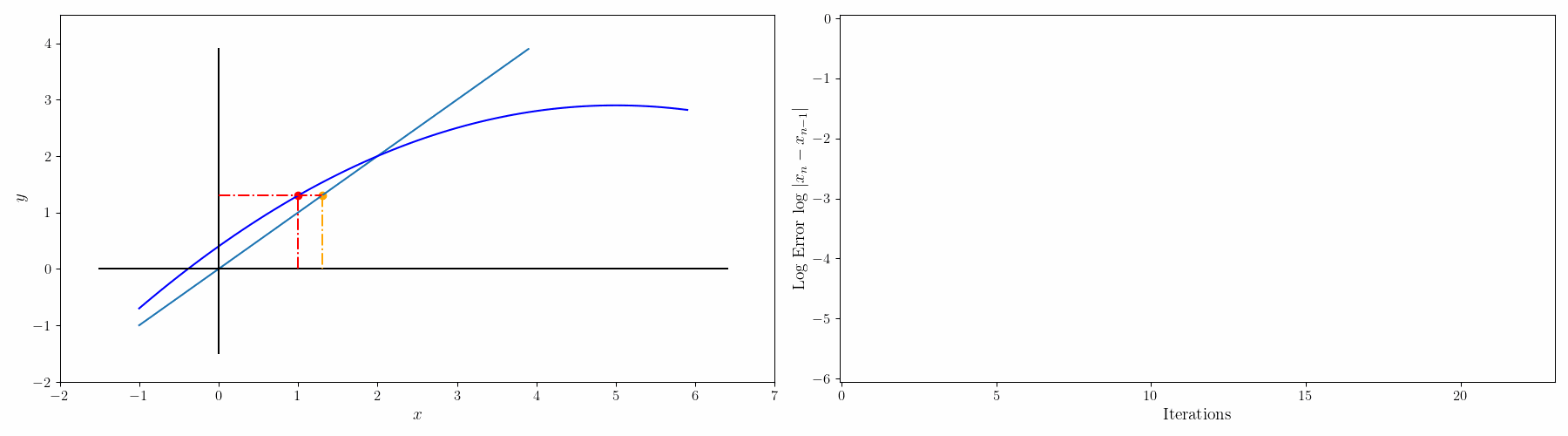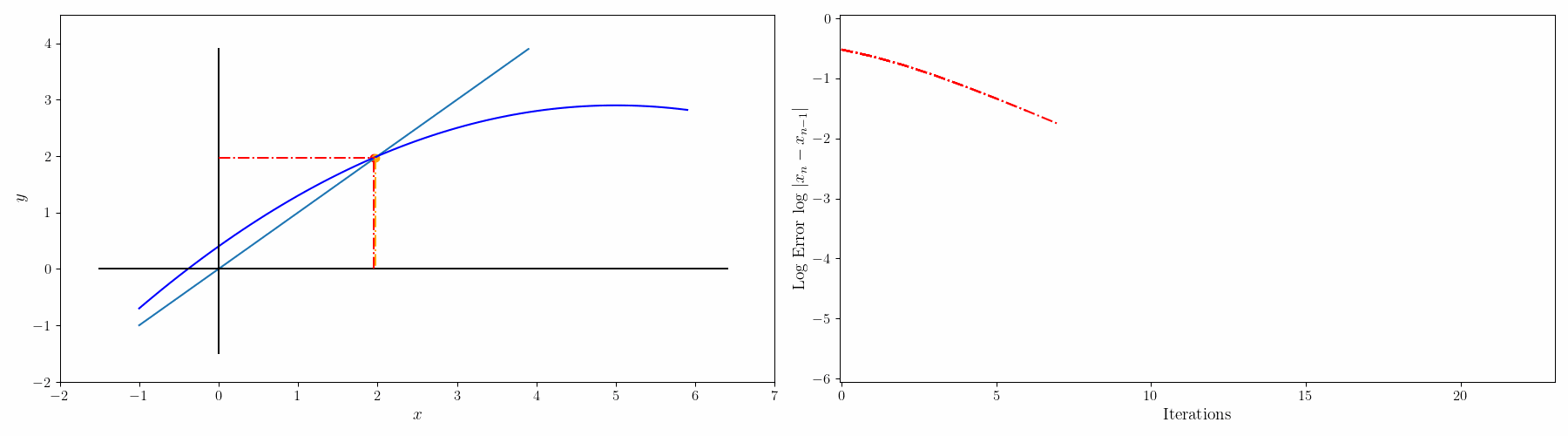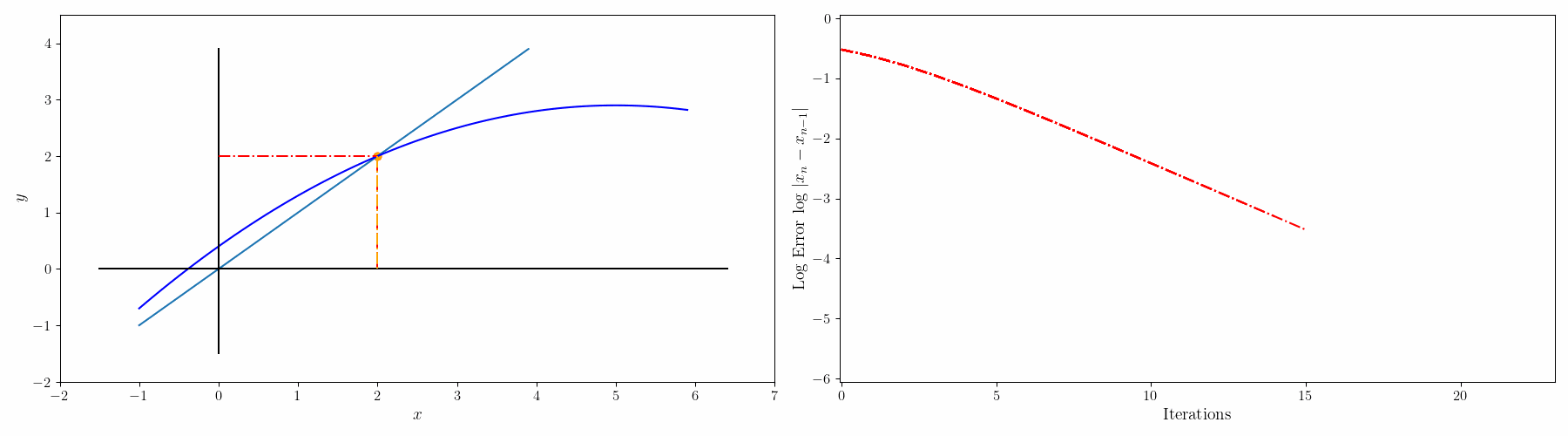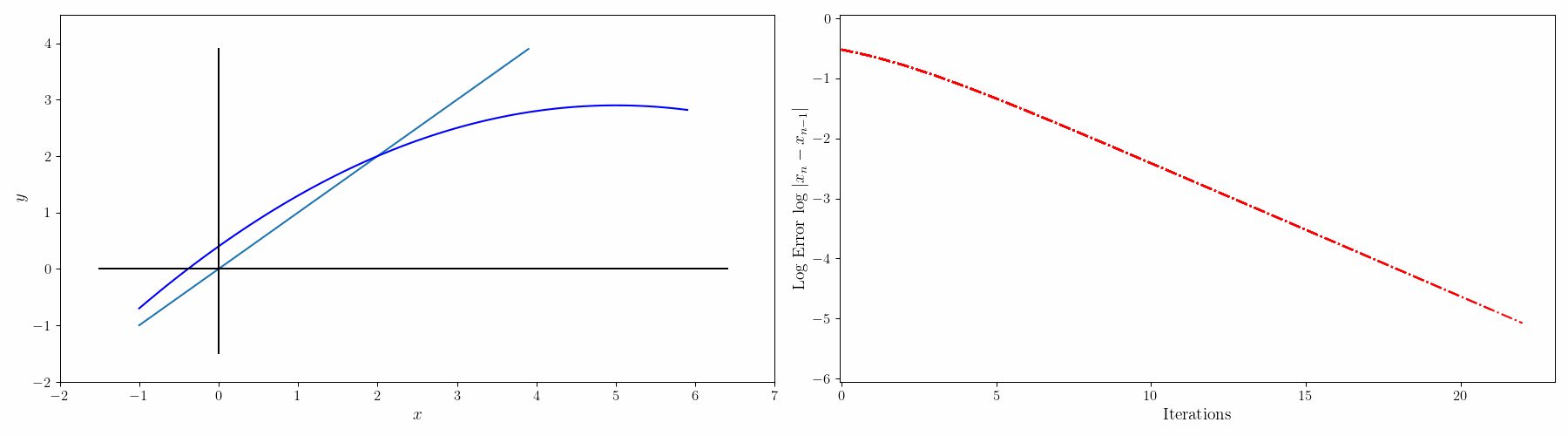
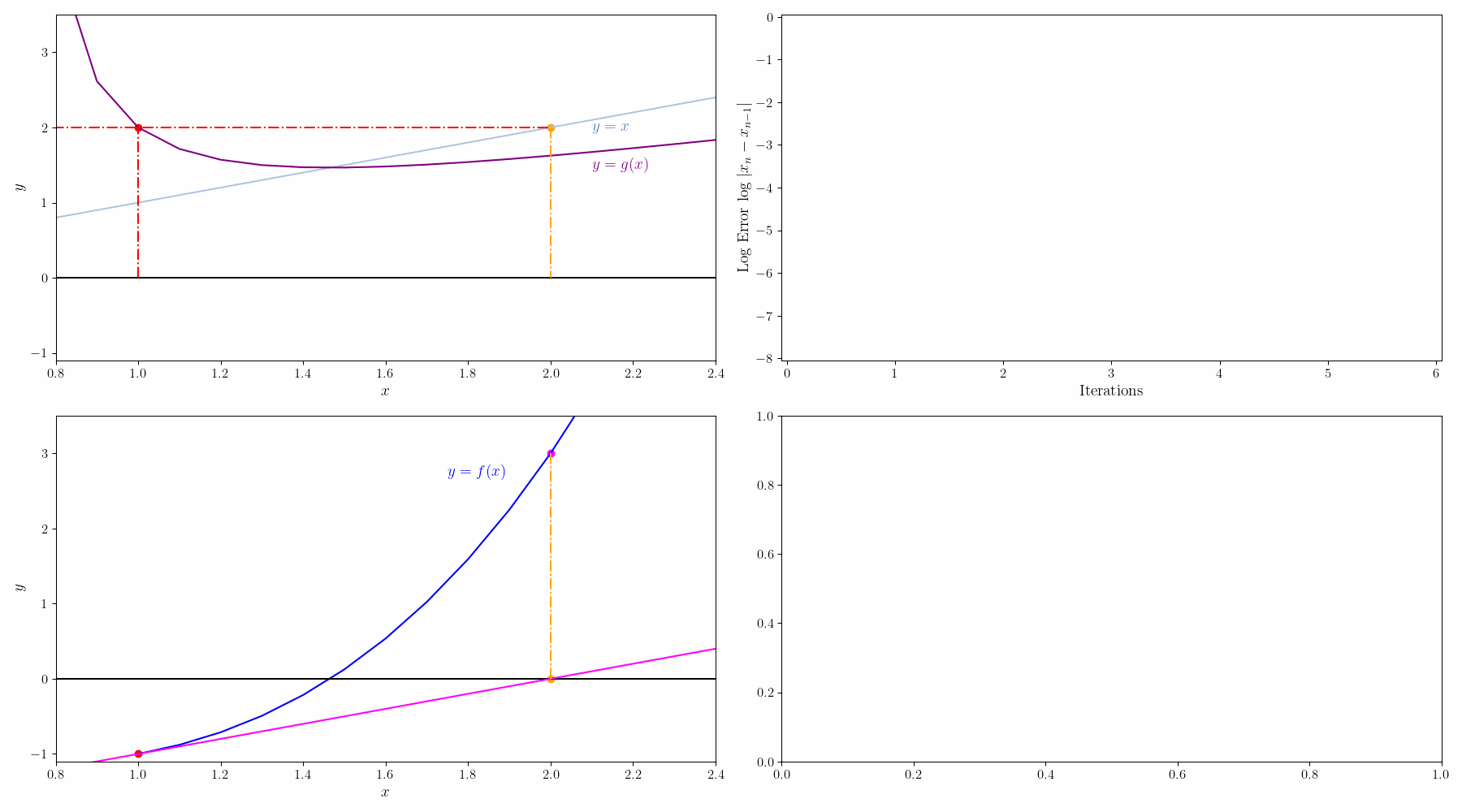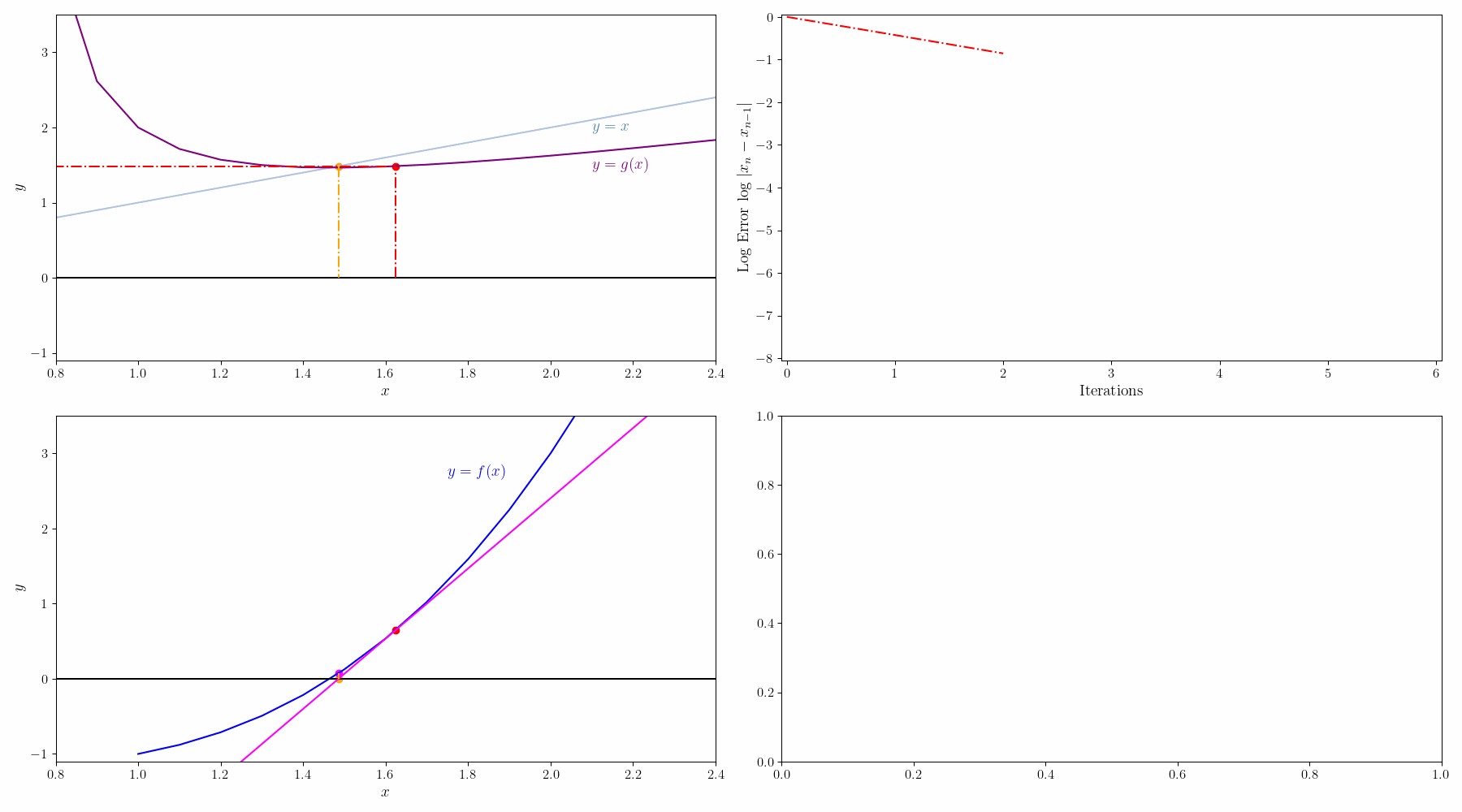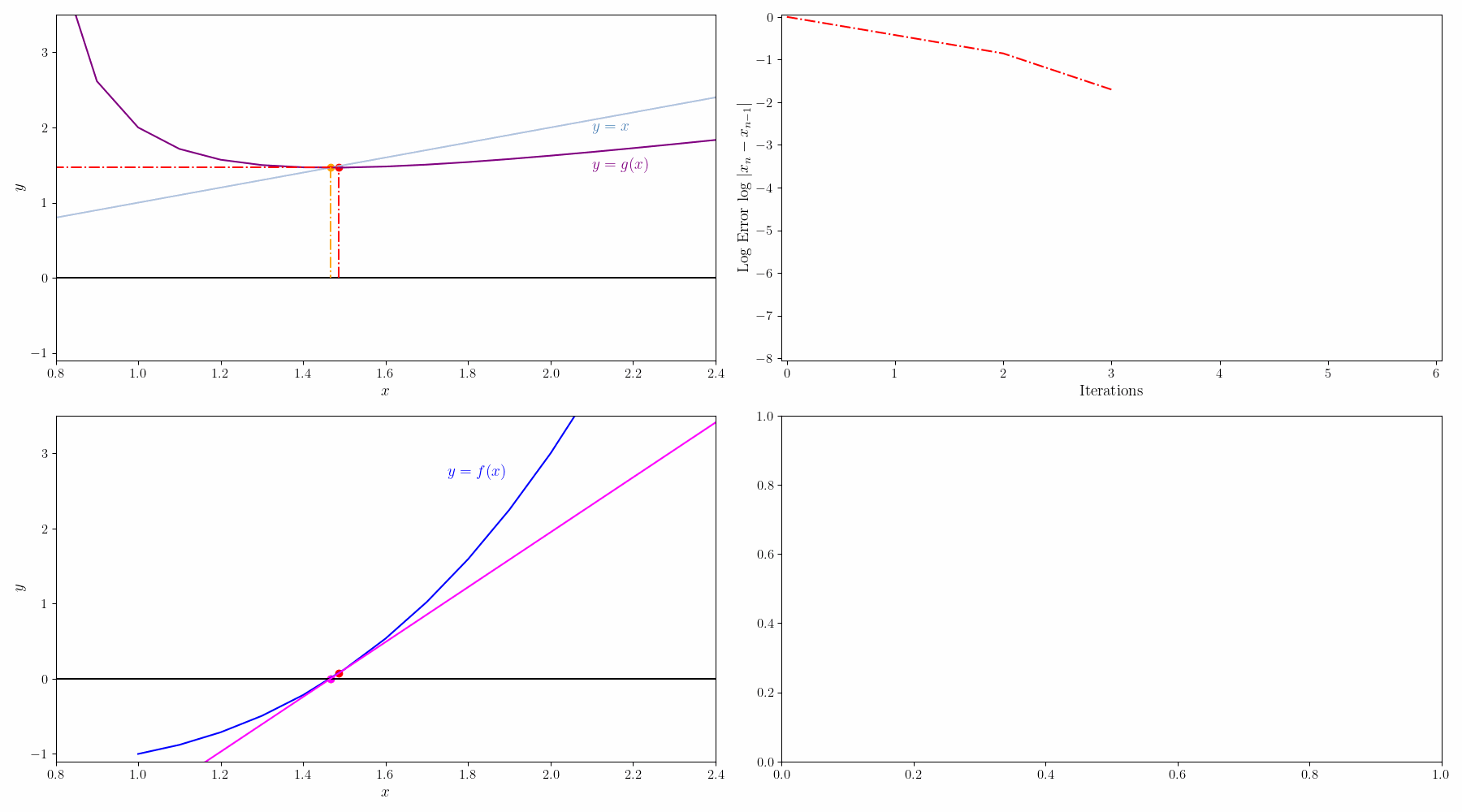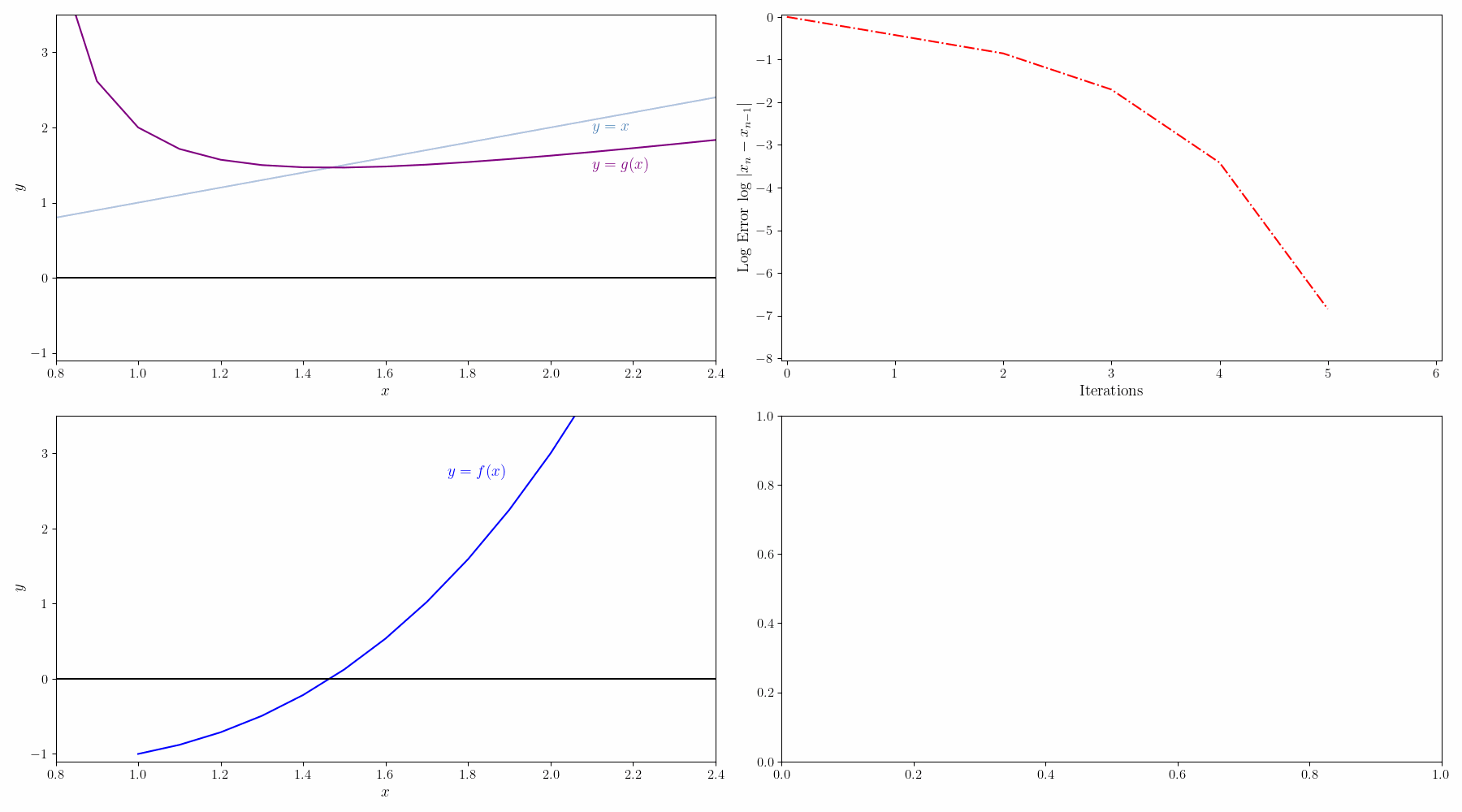
$f(x)=0$를 $g(x)=x$로 변경하면 solution x는 g(x)=y 그래프와 x=y 그래프의 교점이 된다. 초기값 $x_0$에서 시작해서 $g(x_0) = y_0 \rightarrow x_1 = y_0$ $g(x_1) = y_1 \rightarrow x_2 = y_1$ 이런식으로 반복하면서 $x_n=y_n$ 이 되는 점을 찾는다. 예를 들어 $f(x)=0.4-0.1x^2=0$을 고정점 반복법으로 풀어보자. 일단 양 옆에 $x$를 더해서 $g(x)=0.4+x-0.1x^2=x$ 형태로 바꿔줄 수 있다. 그리고 나서 해를 구하는 과정을 그래프로 그리면 아래와 같다.

Newton's method (뉴턴법)

초기값을 선택하고 그 점에서 함수의 접선이 $x$축과 만나는 점이 다음 번 trial 값이된다. 자세히 살펴보자.

$f(x^*)$, when $f(x=x^*)=0$에서 taylor expansion은 아래와 같다.

$f(x)=p_{\infty}(x)=0$

$p_n(x) = f(x^*)+(x-x^*)f'(x^*)+\frac{(x-x^*)^2}{2!}f''(x^*)+\cdots+\frac{(x-x^*)^n}{n!}f^{(n)}(x^*)$

first order approximation은

$f(x) \approx f(x^*)+(x-x^*)f'(x^*)=0$

이고 이걸 우리가 구하고자 하는 solution $x^*$에 관해서 정리하면 아래와 같다.

$x^*=x+\frac{f(x^*)}{f'(x^*)}$

근데 앞의 반복법처럼 $g(x) = x$ 꼴로 바꿔보면

$x=x^*-\frac{f(x^*)}{f'(x^*)} = g(x)$

$x^*$를 어떤 초기값 $x_0$으로 가정한다.

그러면 위의 반복법 과정과 같이

$g(x_0) = x_0-\frac{f(x_0)}{f'(x_0)}=y_0 \rightarrow x_1 = y_0$

$g(x_1) = x_1-\frac{f(x_1)}{f'(x_1)}=y_1 \rightarrow x_2 = y_1$

이런식으로 반복하면서 $x_n=y_n$ 이 되는 점을 찾는다.

장점은 수렴 속도가 매우 빠르고 실수 및 복소수 근도 모두 구할 수 있다.

단점은 근을 찾을 수 있다는 것이 보장되지 않음. 초기값에 의존하기 때문에 초기값을 잘 골라야 한다.

$f'(x) \approx 0$ 인 경우에 해를 찾기 어렵다.

$f(x)/f'(x)$의 부호가 진동하는 경우 (구간 내에 변곡점이 있는 경우)에 해를 찾기 어렵다.

Secant method (할선법)

뉴턴법을 적용할 때 도함수 $f'(x)$를 구해야한다. 도함수를 구하기 힘든 경우가 있기 때문에 secant method에서는 가위치법과 유사하게 두 점 사이의 기울기를 이용한다. 따라서 할선법에서의 도함수 $f'(x)$는 아래와 같이 두 점, $x_{n-1}$과 $x_n$ 사이의 기울기로 설정된다.

$f'(x) \approx \frac{x_n - x_{n-1}}{f(x_n)-f(x_{n-1})}$

이를 뉴턴법의 $g(x)$에 대입하면

$g(x) = x_{n}-f(x_{n})\frac{x_n - x_{n-1}}{f(x_n)-f(x_{n-1})} = x_{n+1}$

이 된다.

할선법은 가위치법과 유사해 보이지만 가위치법에서의 구간 조건, 구간 $[a,b]$에서 $f(a)$와 $f(b)$의 부호가 달라야 한다, 이 없어도 된다. 아래 그림에서 보이는 바와 같이 $x_{n-1}$과 $x_{n}$의 간격에 따라서 $g(x)$ 그래프 형태가 달라진다.