Complex Step

Complex step은 수치 미분값을 구하는 방법 중에 하나다. finite differencing을 유도할 때 small step $h$으로 real number가 아니라 imaginary로 취하고 Taylor expansion을 적용하면 아래와 같다. $$f(x+ih) = f(x) + ihf'(x) - \frac{h^2}{2}f''(x)-\frac{ih^3}{3!}f'''(x)+\cdots$$

여기서 imaginary part만 모아서 보자. $$\text{Imag}[f(x+ih)] = hf'(x) - \frac{h^3}{3!}f'''(x)+\cdots$$

위의 방정식을 $f'(x)$로 정리하면 아래와 같다. $$f'(x) = \frac{\text{Imag}[f(x+ih)]}{h} + O(h^2)$$

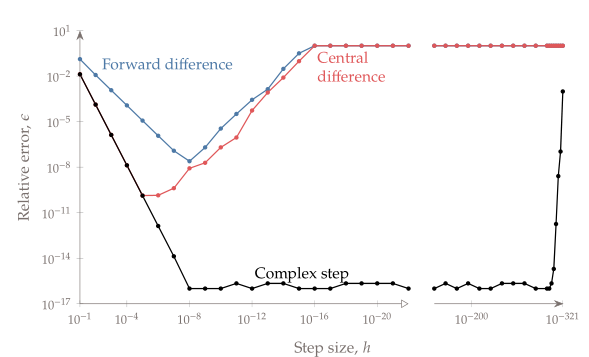
앞에서 finite differencing에서는 step의 크기가 줄어들면, analytic solution과 비교하였을 때 derivative 값의 오차가 줄어들다가 어느 순간이되면 numerical error로 인해서 (subtraction에 의한 significant number의 문제) step이 줄어들어도 error가 커지는 현상이 발견된다. complex step 방법도 step $h$를 이용하지만 finite differencing과 같은 문제가 발생하지 않고 machine precision까지의 정확도가 보장된다. (아래 그림 참고)

변수의 갯수가 늘어나면 계산 횟수가 늘어나는 것은 finite differencing과 같다. 오차의 order를 생각하면 central differencing 이랑 비슷하다.