Gradient-free Optimization

Apr 14, 2022 · 읽으시는데 6 분 걸립니다. ·

Gradient-Free Optimization

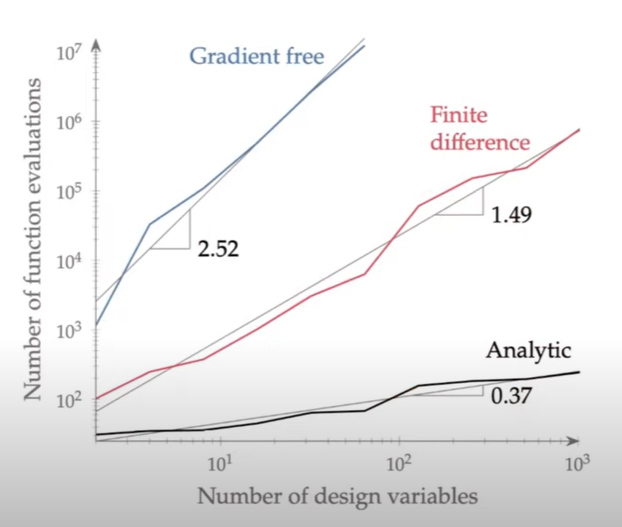
이건 언제 사용하는 거냐? gradient가 계산하기 복잡하거나 계산을 할 수 없는 경우(function evaluation 값이 noisy하거나 아니면 목적 함수가 continuous 하지 않거나, 블랙박스로 싸여있는 legacy 코드라 고칠수가 없는데 noisy하거나 어떤 값이 나오는지 알 수 없을 경우거나, 어떤 경우에 아예 에러가 나오는데 최적화를 수행해야 할 때)에 gradient-free optimization이 유용하게 사용될 수 있다. multi-modal function을 최적화 할때 gradient-free optimization을 사용하여 global optimum을 얻기도 하는데 gradient-free optimization이라고 해서 모든 방법이 global optimum을 주는 것은 아니다. (좀 더 정확하게 말하자면 gradient-free optimization이 global optimum을 찾는데 더 효과적이라고 하겠다.) 그리고 multi-objective optimization에서도 잘 활용될 수 있다. 하지만 그림에서와 같이 design variable의 수가 늘어나면 gradient free optimization의 fuction evaluation의 수가 크게 늘어나므로 비효율적이라고 할 수 있겠다.

Solution methods

Nelder Mead

Nelder Mead는 nonlinear simplex method라고도 하는데 여기서 somplex란 hypertetrahedron이라고 2차원에서는 삼각형, 3차원에서는 피라미드 형태를 띄는 도형이다. Nelder Mead에서는 이 도형의 vertices가 decision points (design variables의 특정 값)가 된다. 따라서 design variable의 수에 따라서 hypertetrahedron의 차원이 달라지는 것이다. 이 방법은 gradient free method이니까 derivative가 필요 없다. 하지만 global minimum을 보장하지 않는 local method이다. problem size가 작으면 (less than 10 dimensions) 비교적 효율적이지만 design variable의 수가 커지면 굉장히 비효율적이다. constraint를 handling할 때 명시적으로(explicitly) 할 수가 없는 단점이 있다.

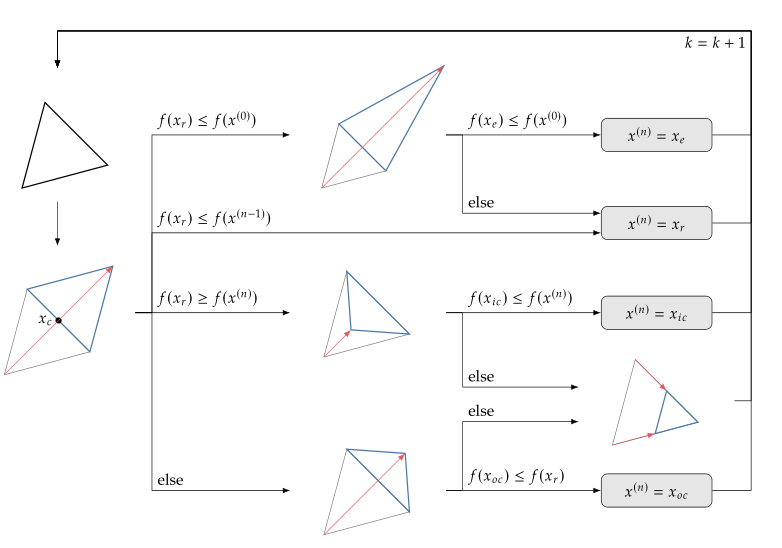
optimum searching 방법을 좀 더 자세히 살펴보면 아래의 그림과 같다. 2차원 문제를 가정하면 왼쪽의 삼각형의 각 꼭지점의 x, y 축 position 값이 design variable의 값이라고 생각하자. 그래서 일단 저 검정 삼각형의 꼭지점 3점에서 function evaluation을 하고 가장 worst를 찾아서 그 점을 reflect 시킨다. 그러면 왼쪽 아래의 파란색 삼각형이 만들어 진다. 그리고 나서 다시 새로운 점에서 목적함수 evaluation을 해서

refelcted point에서의 목적 함수값이 이전 original 삼각형 vertex에서의 목적함수 평가 결과보다 좋을 경우 (여기서 좋을 경우란, minimization하고 있다면 목적함수 값이 더 작아진 경우를 말하고 maximization하고 있아면 목적함수 값이 더 커진 경우를 말한다.) Refelected point가 놓인 방향으로 확장하는 것이 더 좋은 결과를 얻을 수 있다는 것이므로 reflected point를 더 멀리, (이전 point에서 reflected point가 놓이게된 방향으로 더 긴 거리로) 확장한다.

이걸 수학적으로 나타내면, 일단 삼각형 꼭지점들 중에서 worst point를 제외하고 centroid를 구한다. 그림에서 이 centroid는 $x_c$라고 표기되어 있는데 x, y 좌표랑 헷갈리니까 나는 $p_c$라고 표기하겠다. 그리고 design variable의 갯수는 총 $n$개 이다. $$p_c = \frac{1}{n} \sum_{i=0}^{n-1} p^{(i)}$$ 그럼 the worst point $p^n$의 reflected point $p_r$은 아래와 같이 표시된다. $$p_r = p_c + \alpha (p_c-p^{n})$$ 이때 $\alpha$ 값은 '1'이다. 그리고 reflected point를 확장한 점의 위치는 $\alpha =2$를 대입하여 계산해 주면 된다.

refelcted point에서의 목적 함수값이 이전 vertex값보다는 개선되었지만 original 삼각형에 있던 다른 vertex에서의 목적함수 평가 결과보다는 좋지 않은 경우 삼각형 바깥쪽으로 outside contraction을 한다. 일단 개선되었다는 것은 reflected point가 가는 방향으로 이동하는게 좋긴 좋지만 1)에서와 같이 더 멀리 보내버린다고 해서 크게 개선될 여지가 보이지 않는다는 것임. 차라리 reflction하지 않은 다른 vertices를 이동시키는게 좋을지도 모르니까 ouside contraction 시켜서 reflected point를 너무 멀리 보내지는 않는다.

outside contraction 했을 때의 점의 위치는 reflected point $p_r= p_c + \alpha (p_c-p^{n})$에서 $\alpha$ 값을 '1'보다 작은 값은 positive 값을 취해주면 된다. 주로 $\alpha =0.5$.

Reflected point에서의 목적 함수 값이 이전 original 삼각형의 결과보다 안 좋을 경우 삼각형 안 쪽으로 inside contraction시킨다. reflected point가 놓인 방향이 더 안 좋다는 걸 알고 있으니 아예 반대 방향으로 (original point가 놓여진 방향으로) 확장해서 가야되는데 그렇게 하지는 않는다.(사실 이게 잘 이해가 안됨) 어쨌든 orignal point가 놓여진 방향이 더 좋으니까 reflected point를 orignal point가 놓여진 방향으로 이동시키는 것이긴 하네.

inner contraction 했을 때의 점의 위치는 동일하게, reflected point $p_r= p_c + \alpha (p_c-p^{n})$에서 $\alpha$ 값을 -1과 0사이 값을 취해주면 된다. 주로 $\alpha =-0.5$.

Nelder Mead에서는 위의 절차를 반복해서 최적값을 구한다.

Genetic Algorithm (유전 알고리즘)

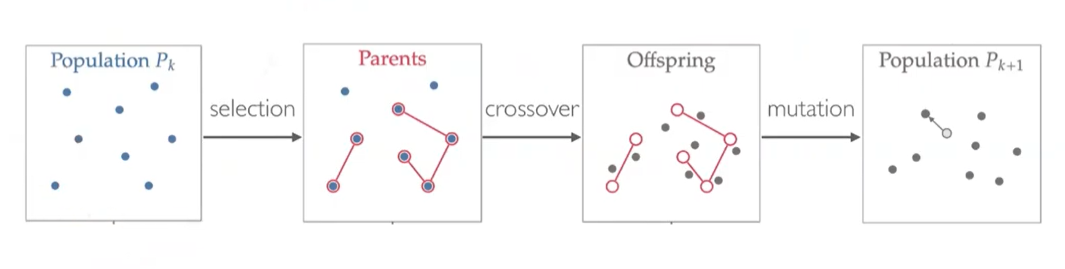
일단 Genetic algorithm은 evolutionary algorithm (진화 알고리즘)의 한 종류이다. 이 evolutionary algorithm은 생물의 진화과정을 본따서 mutation, crossover, reproduction 같은 과정을 통해서 최적해를 찾는 방식이고 그 안에 evolution strategy (진화전략), genetic algorithm (유전 알고리즘), evolutionary programming (진화프로그래밍) 등이 있다. 그래서 evolutionary algorithm은 특정 알고리즘이 존재하는 게 아니고 카테고리를 말한다. genetic algorithm이랑 evolution stratege을 비교하면, crossover가 일어나면 genetic algorithm이고 crossover가 일어나지 않고 mutation만으로 다음 세대를 형성하는 것이 evolutionary algorithm이라고 생각하면 된다. 그럼 이 crossover나 mutation 뭐 이런게 뭐냐하면.... 그림에서와 같이 처음 Population $P_0$라는 것을 random하게 만들어 내는데 이것이 최적화의 design variables를 여러 set 생성시키는 거라고 보면 된다. 이 design variables의 set을 가지고 objective function evaluation을 한 후에 그 중에서 우수한 것들을 selection (선택) 절차를 거쳐서 Parents node (부모노드)로 설정한다. 이 Parents node 간의 crossover (교배)를 통해서 Offspring node(자식노드)들을 만들고 그 offspring 들 중에서 일부는 mutation (변이 혹은 돌연변이)를 일으켜 다음 번 design variables의 set인 Population $P_{1}$을 얻는다. 이러한 과정을 generation이라고 하고 이 generation을 거듭할 수록 population의 목적함수 값이 최적값으로 다가간다.

Genetic algorithm은 binary와 real number 두 분류로 또 나뉜다. population을 이루는 design variables를 binary로 encoding and deconding하는 과정을 거치면서 실수를 binary로 변환해 주면서 최적화를 수행하는 것을 binary genetic algorithm이라고 한다. 이런 과정에서 Hamming cliff라는 것이 생기는데, 예를 들어서 '7' 이라는 정수를 binary로 변환하면 '0111'이고 그것보다 1이 큰 '8'의 경우에 binary로 표현하면 '1000'이다. 따라서 이 경우 정수값으로는 가까운데 binary 값은 4 자리의 값 모두를 flip 해주어야 하므로 교배의 과정을 거쳐서 생성하기 어렵다. 이런 것을 Hamming cliff라고 한다. 그리고 binary GA에서 '0'과 '1'만을 사용하지만 실제 우리는 고급 프로그래밍 언어에서 코딩하니까 machine precision을 다 쓸 수가 없다. 하지만 discrete variables에 사용하기 편하고 crossover가 real number GA 에서는 크게 자연적 의미가 없는 그저 과정인데 binary GA에서는 그래도 조금 더 parents의 특성을 가져갈 수 있는 의미를 가지게 된다. 어쨌건 real/binary GA 둘 다 stochastic한 접근이고 huristic한 방법이다.

Particle Swarm

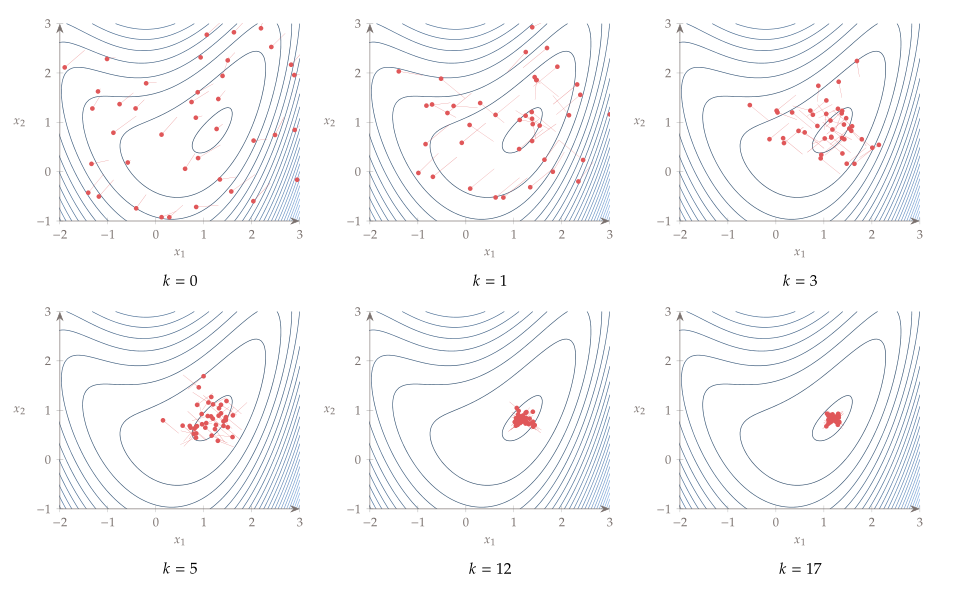
Particle Swarm Optimization (PSO)는 새의 무리나 물고기 집단의 움직임을 모방한 최적화 방법이다. 따라서 일단 새 무리나 물고기 집단처럼 개체가 어떤 영역에 여러개 흩어져서 자기 마음대로 움직이고 있는 것을 생각해 보자. 이 개체 하나 하나가 design variables의 조합이라고 생각하면 된다. (뭔가 말이 좀 헷갈리는데, 예를 들어서 문제에 design variable가 하나이고 0과 10 사이의 어떤 값을 갖는다고 가정하면, 개체1은 0, 개체2는 1.5, 개체3은 5.3 뭐 이렇게 각자 다른 design variable 값을 나타낸다고 생각하면 된다. 말이 좀 헷갈리게 쓰여져 있는 이유는 design variable이 하나가 아닐수도 있어서 인데, 예를 들어 0과 10사이의 실수 두 개 라고 하면 개체1은 (0, 7.8) 개체2는 (2.5, 5,9) 뭐 이런식이라는 거지) 일단 개체들이 흩어져 있는 상태에서 각각 목적함수 평가를 한다. 그리고 난 다음에 다른 곳으로 이동해야할텐데 이 각각의 개체들은 각자의 velocity (vector값)라는 것을 가지고 있어서 원래 이동하던 방향이 있는다. 이것을 inertial라고 하고 이전에 이동했던 방향에 영향을 받는다. 그런데 목적함수의 값이 좋아지는 쪽(최소화의 경우 목적함수 값이 작아지는 쪽, 최대화의 경우 목적함수 값이 커지는 쪽)으로 이동해야 최적값을 찾을 수 있으므로 여기에 memory와 social이라는 두 개의 개념이 추가된다. memory는 각각의 개체가 각자 이동하다가 가장 좋았던 장소를 기억하는 것이고 social은 개체가 모인 집단 전체에서 가장 좋은 장소를 참고하는 것이다. 이 inertial, memory, and social의 방향의 vector 합이 개체가 다음으로 이동할 방향을 나타내고 이 vector의 크기가 최적화 과정에서 점점 줄어들면서 개체들이 하나의 최적해로 몰리게 된다.

아래 그림이 이 과정을 나타내고 있다. 빨간색 점들이 각각의 개체이며 그 점들에 붙은 실선들이 개체가 이동하는 방향의 vector이다.