Multiobjective Optimization

최적화 문제에서 목적함수 objective가 여러개 (주로 2, 3, 4정도) 있는 경우에 다목적 최적화 multiobjective optimization 를 수행한다. 근데 결국에는 하나를 선택해야 될 것인데 왜 다목적 최적화가 필요한 것인가? 그 이유는

1. objectives의 tradeoff를 quantify 할 수 있기 때문이다. - 보통 objectives 들에 어떤 커플링이 있는데 mutliobjective optimization을 통해서 design variable의 변화에 대한 objectives의 sensitivty 를 알 수 있어서 최종 결정에 도움을 줄 수 있다.
2. 실제로 하나의 design을 하는게 아니라 여러 option을 어떤 executive committee 같은 곳에 제시해야 하는 경우가 있다. 이런 선택지를 family of design 이라고 할 수 있지.
3. underlying objective가 계산할 수 없거나 너무 complex해서 계산하기 어렵거나 할 때 objective를 분리하여서 여러가지 옵션을 보는 것임

따라서 다목적 최적화의 해는 하나로 결정되지 않고 어떤 집합으로 나오는데 그걸 Pareto front 라고 한다. 아래의 그림에서 함수 $f_1$과 $f_2$가 obective values 이며 $f_1$과 $f_2$ 둘 다 작은게 좋은 거라면, 빨간색으로 표시된 점들이 pareto optimum 값들이며 non-dominated set, pareto front, pareto optimum, pareto set 이라고도 불린다. 이 non-dominated set 사이에는 어떤게 더 좋은지 알 수 없다. 하지만 파란색으로 표시된 점들과 빨간색 점을 비교하면 파란색 점들은 dominated 되었다고 하고 빨간색 점들 중에 어떤 하나는 반드시 이 파란색 점들보다 $f_1$과 $f_2$ 두 함수의 관점에서 더 나은 값이 있다.

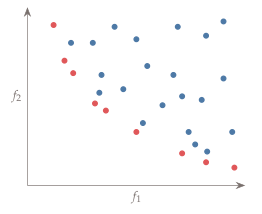
Solution methods

Weighted sum

Objective 각각에 weight을 곱하고 더해줘서 single optimization으로 만들어서 푸는 방법이다. 새 objective function은 $$\begin{aligned} \overline{f}(x) &= \sum_{i=1}^{n_f} \omega_i f_i (x) \newline \sum_{i=1}^{n_f} \omega_i &= 1 \end{aligned}$$

Weight을 변화시키면서 pareto set을 만들수 있는데 이 방법에서는 weight을 어떻게 선택하느냐가 문제다. 그리고 pareto front의 모양에 따라서 어떤 구간의 pareto front를 아예 얻지 못할 수도 있다.

Epsilon-constraint Method

하나의 objective를 남겨두고 다른 objective를 constraint로 취급하여 single optimization을 푸는 방법이다. objective를 이용하여 constraint를 구성할 때 epsilon을 inequality constraint의 bound로 설정한다. 이것을 수학적으로 표현하면 아래와 같다. $$\begin{aligned} \underset{x}{\text{minimize}} \quad & f_i \newline \text{subject to} \quad &f_j \leq \epsilon \quad \text{for all } j \neq i \newline &g(x) \leq 0 \newline &h(x) = 0. \end{aligned}$$

Weighted sum에서 weight은 physical meaning은 없는 parameter이지만 여기서 $\epsilon$은 constraint로 취급되는 objective의 제약값이 된다. ($\epsilon$ 설정하려면 physical sense가 필요함) 그리고 weighted sum에서 pareto front의 모양에 따라서 놓칠 가능성이 있었던 pareto front 값을 epsilon-constraint에서는 구할 수 있다. 하지만 여전히 $\epsilon$ 을 어떤 간격으로 설정할지가 문제이다.

Normal Boundary Intersection

Epsilon-constraint 방법의 $\epsilon$ 간격 설정 문제를 해결하기 위해서 제안된 방법이다. 그래서 epsilon-constraint 방법과 비슷한다. pareto front의 두 끝점에서 linear line을 그어서 evenly spacing하고 거기의 normal한 방향에서 pareto front랑 만나는 점을 구할 수 있는 $\epsilon$을 설정한다는 건데 자세한 건 잘 모르겠다. 아마도 다른 사람들도 어렵다고 생각해서 epsilon-constraint을 많이 쓴단다. 그렇지만 objective의 수가 많은 경우 normal boundary intersection이 좀 더 좋을 수 있다는데 왜인지 잘 모르겠음.

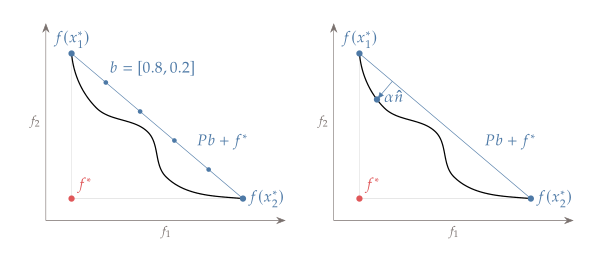
Evolutionary Algorithm

Evlotionary algorithm에서는 genetic algorithm에서 설명한 방법으로 최적화를 수행한다. single objective gradient free optimization과 다른 점은 population evaluation을 통해서 구해진 해를 탈락시키지 않고 다 가지고 있다는 것이다. 이 해들 간의 비교를 통해서 sorting하고 tournament 형식으로 non-dominated set을 찾아낸다. evolution을 반복하면서 이 sorted set을 업데이트 해 나가는데, sorted set 내부의 preto front들 사이에는 sorting하여 줄을 세울 수가 없으니까 rank라는 개념을 또 도입한다. solution의 밀도가 높은 지점을 제외하도록 밀도가 낮은 지역의 ranking을 높게 준다. 여기서 밀도 평가하는 함수를 crowding distance라고 한다. 그래서 여튼 evolution이 진행될수록 이 ranking이 높은 것이 앞으로 간 non-dominated set이 sorted set에 남아 있게 된다.

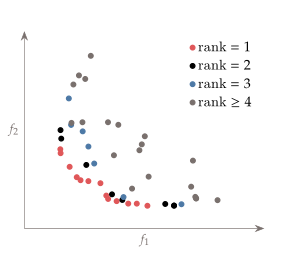
Gradient free method가 갖는 단점을 그대로 이어받아서 최적화 해를 얻는 시간이 많이 들지만 design variable의 갯수가 적을 때에는 앞에서 서술한 다른 방법들보다 좋을 수 있다.