Sampling Methods
Sampling Methods
sampling method 중에서도 optimization에서 주로 쓰이는 방법은 random sampling, Latin Hypercube Sampling(LHS), Low-discrepancy sequences 중에 하나인 Halton sequence이다. ramdom sampling은 그냥 random하게 sample을 선택하는 방법인데 이게, 도메인을 골고루 커버하지 못 할수가 있다. 특히 sampling 수를 줄이면 결과가 더 안좋은데 그래서 Latin Hypercube Sampling이 이를 개선한다.
Latin Hypercube Sampling
일단 LHS의 결과를 보면 아래 그림과 같다.
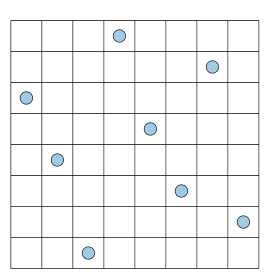
가로축으로 한 칸 한 칸씩 이동하면서 보면 완전히 비어 있는 열이 없고 세로축으로 한 칸 한 칸씩 이동하면서 봐도 완전히 비어있는 행이 없다. 이렇게 되려면 일단 가로로 봤을 때 각 열(column)들에 sample이 존재할 활률이 균일해야한다. 즉 uniform distribution이어야 한다. 세로로 봤을 때도 마찬가지니까 그림으로 그리면 아래와 같겠다.
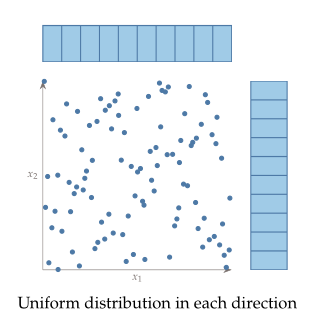
근데 이렇게만 정해 놓으면 아래 그림과 같이 sample이 선택되는 불상사가 생길 수도 있다.
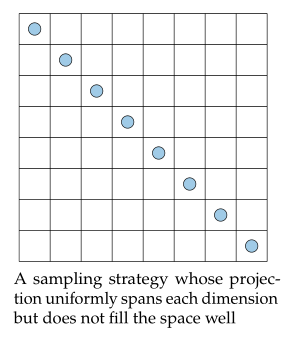
그럼 뭘 추가해야되냐면 각 sample간의 거리를 maximize 해야 된다. 그래서 정리해 보면 sample을 각 축으로 projection했을 때 uniform distribution을 따라야하고 sample간의 거리는 최대화 되어야 한다. (여기서 꼭 uniform distribution일 필요는 없다. optimization domain의 특성을 잘 알고 있으면 거기에 맞게 다른 distribution을 적용할 수 있다.)
이건 어디다 쓰냐? Genetic algorithm이나 Praticle Swarm, multi start gradient-based optimization의 starting point를 정할 때 쓸 수 있고 Monte carlo method, surrogate model 만들때도 쓸 수 있다.
Halton sequence
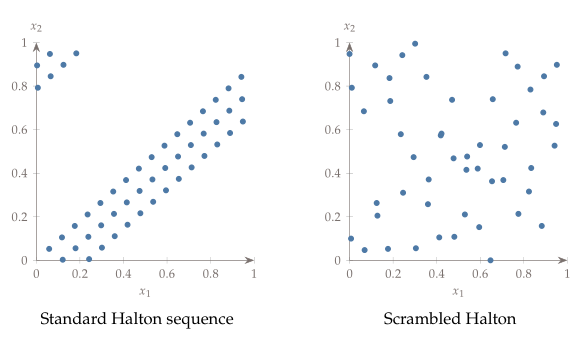
Halton sequence는 low discrepancy sequences 중에 하나 인데 여기서 low discrepancy는 sample을 생성하고 도메인이 표시했는데 어떤 작은 영역 여러개를 설정하여 그 것들 안에 있는 sample의 밀도를 비교해 보아도 크게 차이가 없다는 뜻이다. 그래서 well spreaded를 의미하는 것임.
여기서 sequence도 중요한데, LHS의 경우에 sample 30개를 만들어서 function evaluation하고 난 다음에 sample 50개를 생성해서 비교하고 싶은데 앞전에 만들었던 set이랑 완전히 다른 50개의 sample이 생성된다. 근데 low discrepancy sequences는 sample 갯수가 30개에서 50개로 늘어나면 앞에 있던 sample set을 포함하는 set을 만들 수 있다. 그래서 iterative method에 사용하기 적합하다.
그래서 앞에서 설명한걸 그림으로 보면 아래와 같다. i는 sample의 갯수를 나타내는데 sample의 갯수가 늘어나면서 새로 추가되는 sample이 파란색으로 표시되었다.
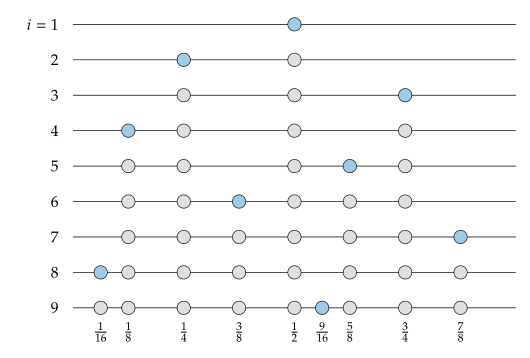
이 i를 나타내는 아래의 식과 같은 sequence 라고 하자.
$$i = a_0+a_1b+a_2b^2+ \cdots + a_rb^r \quad \text{where } a \in [0, b-1] $$
여기서 base $b$는 어떤 값으로 주어지고 coefficient인 $a$를 i의 설정에 따라서 구하게 된다. a를 구하고 난 다음에 Halton sequence에서는 아래의 연산을 통해서 i번째 sample의 값을 결정한다.
$$\phi_b(i)=\frac{P_{a_0}}{b}+\frac{P_{a_1}}{b^2}+\frac{P_{a_2}}{b^3}+\cdots+\frac{P_{a_r}}{b^{r+1}}$$
여기 나오는 $P_{a_i}$는 또 뭐냐면 $P=[0,1, \dots, b-1]$처럼 생긴 ramdom integer permutation (순열)인데 계수 $a_i$를 그대로 쓰지 않고 ($a_i$를 그대로쓰면 아래 그림의 왼쪽에 standard Halton sequence처럼 sample이 형성됨)이 permutation의 index라고 생각하고 순열에서 $a_i$번째에 있는 element를 꺼내와서 Halton sequence 계산에 분자로 쓴다. 그러면 아래 그림의 왼쪽에 Scrambled Halton이라고 표시되어 있는 그래프처럼 sample point들이 잘 퍼져있는 sample set이 형성된다.