Discrete Optimization
Discrete Optimization
Optimization의 Design variables가 discrete한 문제를 discrete optimization problem이라고 한다. 이는 discrete variable의 종류에 따라 3가지로 분류될 수 있다.
- binary (0 or 1)
- integer (vehivle의 wheel의 갯수 등을 선택하는 문제)
- discrete (예를 들어 금속의 종류를 선택한다거나 등의 문제)
discrte opimization은 nondeterministic polynomial time complete 이므로 solution이 최적인 것을 verify할 수 있지만 solution을 효율적으로 구하는 방법이 없다. 그래서 주로 huristic 한 방법을 이용한다.
Discrete optimization을 피하는 방법
Continuous variable이 discrete variable 보다 더 많은데 이 discrete variable때문에 discrete optimization을 선택해야 한다면 이것을 피하기 위해서 continuous optimization을 돌리고 discrete variable에만 round 하면 됨 그리고 그 variable을 fix한 상태에서 다시 optimization을 돌릴수도 있다. exhaustive search도 continuous variables가 많고 discrete variable의 수가 적은데 그 discrete variable의 선택지가 또 a few 일 때 사용할 수 있다. 이건 뭐냐면 그 a few 선택지의 discrete variable을 fix한 상태에서 continuous optimization을 수행하여 그 결과들끼리 비교하는 것이다. 또 마지막으로 parameterization을 바꾸는 방법이 있는데 discrete variables을 modeling을 달리하여서 continuous variable로 바꾸는 것이다.
Exmaples
1. A greedy algorithm
네트워크 optimization도 discrete optimization이라고 할 수 있는데, 주로 greedy algorithm의 concept을 이용한다. 방금 이동한 곳 주변에서 선택가능한 best option을 선택하면서 다음 단계로 나아가는 것이다. 이건 fast solution이고 반복적으로 수행해도 같은 값으로 수렴하지만 커플링을 무시하므로 아래의 그림에서처럼 global optimum으로 간다는 보장이 없다.
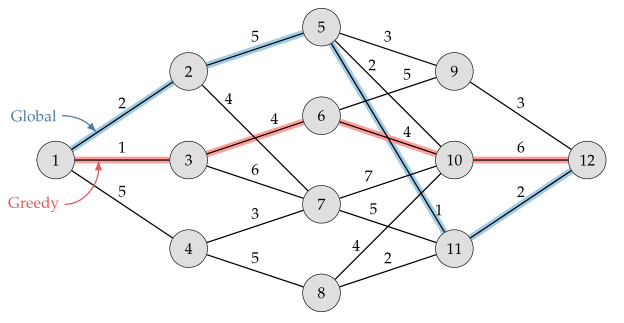
1번 노드에서 출발한다면 cost가 가장 작은 것이 3번 노드로 이동하는 cost=1 이다. 그래서 greedy 알고리즘음 3번 노드로 이동하고 3번 노드에서도 동일하게 cost가 가장 작은 노드로 이동하는 것을 반복하여 최종 노드로 도달하는 방법
2. Branch and Bound
discrete variables의 선택지로 tree를 만들어 tree의 branch를 타고 나가며 최적값을 찾는 방법이다. tree를 prune 해 나가는 과정에서 leaves에 bounded와 infeasible 영역이 형성되어 branch and bound라고 하는 듯. convex integer problem 에 꽤 유용하게 쓰인다.
예를 들어 아래와 같은 문제를 생각해 보자.
$$\begin{aligned}
\text{minimize} \quad & -x_1-2x_2-3x_3-1.5x_4 \newline
\text{subject to} \quad & x_1 + x_2+2x_3+2x_4 \leq 10 \newline
& 7x_1+8x_2+5x_3+x4=31.5 \newline
& x_i \in \mathbb{Z}^+ \text{ for } i=1,2,3 \newline
&x_4 \geq 0.
\end{aligned}$$
$x_i$가 positive integer이므로 discrete optimization인데 여기에 branch and bound method를 이용하여 풀어보자. $x_3$를 시작으로 부등식으로 구성되는 binary tree를 만들어 나가면 아래의 그림과 같다. 여기서 $f^*$가 minimum 이 되고 이때 optimum variable $x^*$는 [0,2,3,0.5]가 된다.
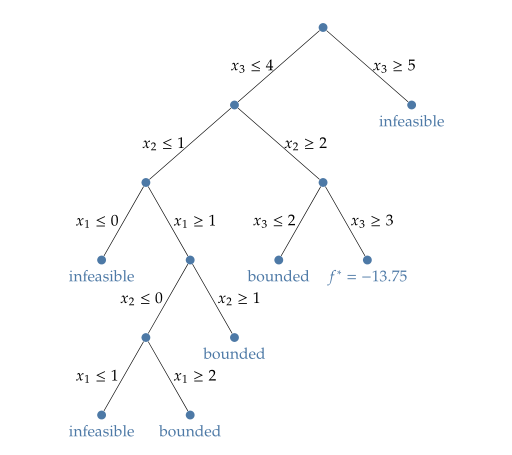
3. Dynamic programming (동적계획법)
Dynamic programming은 하나의 최적화 문제를 여러 개의 subproblems로 쪼개서 이 subproblems의 optimal solution을 찾는 것을 반복하여 전체 proble의 optimimal solution을 찾는 방법이다. 꼭 discrete optimization에서 뿐만 아니라 continuous optimization이나 optimization 이외의 영역에서도 문제에서 반복되는 어떤 특정한 structure를 찾아서 subproblems을 풀면서 전체를 푸는 개념을 통틀어서 dynamic probramming이라고 한다. 알고리즘이라기 보다는 technique라고 하는게 더 맞을 듯. 알고리즘으로 표현할 수가 없다.
앞에서 설명한 gready 알고리즘이랑 비슷하다고 생각할 수 있는데 gready는 현재 상태에 코 앞에 있는 subproblem 하나만 푸는 방식이지만 dynamic programming에서는 전체 영역을 subproblem들이 커버하고 있다. 이것은 dynamic programming의 구조가 Markov chain (continuous problem에서는 Markov process)의 특성 (Property)을 만족해야 하기 때문이다. 여기서 Markov chain의 특성이란 전체 history를 알지 못해도 현재의 state만 가지고 future state를 알아낼 수 있다는 것인데 (마르코브 체인은 현재 state n이 과거 한 단계 전인 n-1 state에 의해서만 결정된다 라고 주로 표현한다.) 이런 Markov property가 만족되면 optimization 문제를 구조화하여 recursive하게 풀 수 있다. (recursion이라 하면 Fibonacchi sequence를 푸는 알고리즘처럼 자기 자신 함수를 불러서 문제를 푸는 것이다.)
주어진 state $s_i$에서 design decision $x_i$를 하면 이때의 cost function은 $c(s_i, x_i)$ 이고 이런 decision이 여러 개이면 현재와 미래의 cost의 sum의 최적값인 value function은 다음과 같이 표현할 수 있다.
$$v(s_i) = \underset{x_i,...x_n}{\text{minimize}} \quad c_{i}(s_i,x_i) + c_{i+1}(s_{i+1},x_{i+1}) + \cdots + c_{n}(s_n,x_n)$$
여기서 n은 우리가 cost를 평가하는 시점이나 구간이다. 이 value function을 recursive procedure로 나타내면 아래의 $\textit{Bellman equation}$과 같다.
$$v(s_i) = \underset{x_i}{\text{minimize}} \quad c(s_i, x_i)+v(s_{i+1})$$
이것이 Bellam의 또 principle of optimality의 수학적 표현이라고 할 수 있겠다.
Principle of optimality란 주어진 문제의 최적해는 subproblem의 최적해들로 구성된다는 것이다.
위의 greedy 알고리즘에서 봤던 graph 문제를 dynamic programming 관점에서 다시 보자

이제는 마지막 도착 노드 12부터 그 앞의 노드 9, 노드 10, 노드 11까지만 있는 subproblem으로 나눠보자.
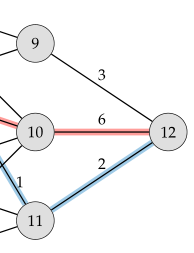
이 상태에서 cost와 next node에 관한 표를 만들어 보면 아래와 같다.
| Current node | 9 | 10 | 11 |
|---|---|---|---|
| cost | 3 | 6 | 2 |
| Next node | 12 | 12 | 12 |
이후에 노드 9, 10, 11과 바로 연결되어 있는 노드 5, 6, 7, 8까지의 subproblem을 보자.
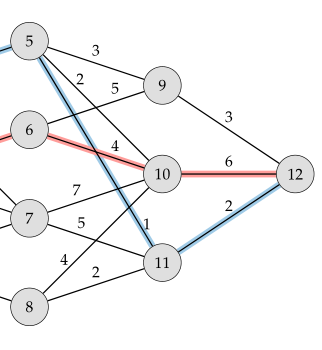
예를 들어 노드 5는 노드 9, 10, 11과 다 연결되어 있다. 노드 9를 거쳐서 노드 12로 이동하면 cost가 3+3=6 이 되고 노드 10을 거쳐 12로 이동하면 cost가 2+6=8, 노드 11을 거쳐 12로 이동하면 cost가 1+2=3 이 된다. 이때 minimum은 노드 11을 거쳐 12로 이동하는 것이니 위의 표는 아래와 같이 수정된다.
| Current node | 5 | 9 | 10 | 11 |
|---|---|---|---|---|
| cost | 3 | 3 | 6 | 2 |
| Next node | 11 | 12 | 12 | 12 |
이런 과정을 반복하면 마지막에 완성되는 표는 아래와 같다.
| Current node | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cost | 10 | 8 | 12 | 9 | 3 | 8 | 7 | 4 | 3 | 6 | 2 | 0 |
| Next node | 2 | 5 | 6 | 8 | 11 | 9 | 11 | 11 | 12 | 12 | 12 | - |
그럼 결과는 1번 노드에서 2번노드 - 5번노드 - 11번 노드 - 12번 노드로 이동하는 cost 10인 route로 나온다. 이게 global optimum!!!

4. Simulated annealing
Optimization 과정에서 design variables을 update할 때 어떤 확률분포에 의해서 design variable을 선택하는 방법이다. local minimum에 빠지지 않고 approximated global optimum을 얻을 수 있다. continuous optimization에서도 보조로 쓰일 수 있겠군...
원래 anealing이라는 것은 금속이나 유리를 불에 달궜다가 천천히 식혀서 강화시키는 것을 말한다. 금속에 열을 가하면 원자가 막 자유롭게 돌아다니다가 천천히 식는 동안에 minimum-energy state로 구조가 변경이 된다. 반대로 금속을 빠르게 냉각하면 금속이 비정질금속(amorphous metal)이라고 불리는 다른 더 높은 에너지 state로 재 결정화(recrystallized)된다.
이건 그냥 맞는지 아닌지 잘 모르겠는 내 해석인데, 금속에 열을 가한다는 것은 design variable을 사방에 흩트려 놓았다가 온도를 천천히 낮추면서 minimum state 향해 가는게 optimum solution으로 다가가는 거라고 보면 그 확률을 조절하는 건거 같다.
시스템이 특정 에너지와 온도로 어떤 상태에 있을 확률을 분포로 나타낸 것을 Boltzmann distribution (Gibb distribution이라고도 함) 이라고 하며 아래와 같은 관계를 갖는다.
$$P(e) \propto \exp \left( \frac{-e}{k_B T} \right)$$
여기서 $e$는 에너지 레벨이고 T는 온도, $k_B$는 Boltzmann 상수이다.
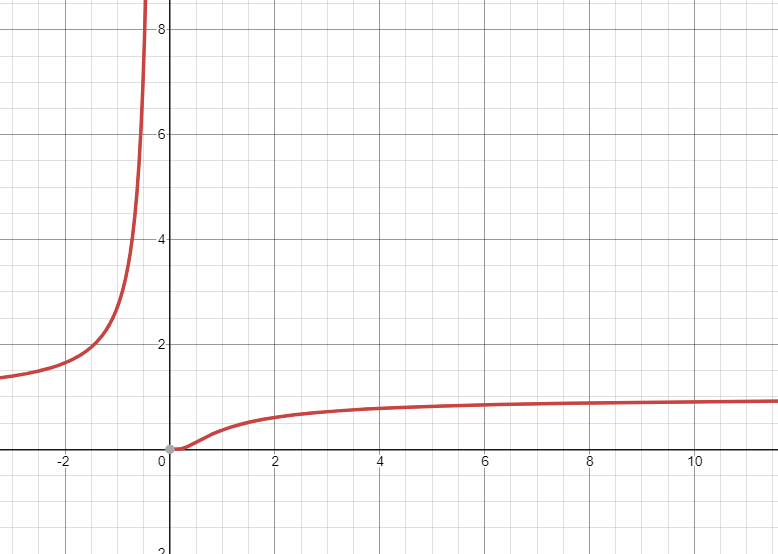
$f(x)=\exp{-\frac{1}{x}}$의 그래프가 아래와 같으므로... 온도 T가 감소하면 높은 에너지 state로 있을 확률이 감소한다. 하지만 절대 0이 되지 않는데 이게 T에 해당하는 parameter가 감소하고 local minimum에 가까워 지더라도 hight envergy level로 점프한다는 거는 design variable의 다양성이 커져서 local mimimum에 빠지지 않게 만들어 준다는 듯
Metropolis–Hastings algorithm 이라는 것이 있는데 probability distribution에서 a sequence of random samples을 구하는 방법이다. 이 알고리즘을 적용하여서 우리가 가지고 있는 probability distribution에서 design variable set을 얻는다.

여기서 P가 위에서 말한 atom의 Boltzmann distribution에 해당하는 건데 우리는 Boltzmann 상수 같은 건 필요없으니까 제외하고 energy level $e$를 objective function value로 생각하면 된다.