Line Search

$$\underset{x}{\text{minimize}} f(x)$$ 위의 식과 같이 constraint가 없는 최적화 문제에 problem domain이 모든 영역에서 differentiable하면 (미분가능, 이건 연속이랑 다른 개념이라는 걸 고딩 때 배우지) 해당 함수의 gradient, $\nabla f = 0$ 지점이 함수의 극 값, 즉 maximum이나 minimum이 된다. 그래서 최적화 문제 풀 때 $\nabla f(x) = 0$ 의 방정식을 푸는데 (이 방정식을 만족시키는 x를 구한다) 이 과정에서 line search가 나온다.

수치해석적으로 $x$를 적절히 이동시키면서 위의 방정식이 어떤 tolerance $\epsilon$ 내에서 만족되면 연산을 정지한다.

1k=0
2while || $\nabla f ||_{\infty} \geq \epsilon$ do
3    search direction $p_k$ 결정
4    step length $\alpha_k$ 결정
5    $x_{k+1} = x_k+\alpha_k p_k$
6    $k=k+1$
7end while

근데 그러면 $p_k$ 랑 $\alpha_k$ 는 어떻게 결정하면 될까? 일단 subproblem으로 다른 변수들은 다 fix한 상태에서 $\alpha$를 구하는 것을 먼저 생각해 보자. $k+1$ 번째 $x$는 $x_{k+1} = x_k + \alpha p_k$ 이므로 이를 함수 $f$에 대입하면 $f(x_{k+1}) = f(x_k + \alpha p_k) = \phi(\alpha)$ 이고, 함수 $\phi$를 step length $\alpha$에 의한 함수로 정의하자. 이 함수 값은 $\alpha = 0$ 일때 $\phi(0) = f(x_k)$ 이므로 (현재 우리가 알고 있는 값) 여기서 $\phi'(0)$ 보다 좀 더 flat한 직선을 그었을 때 $\phi(\alpha)$ 값들이 이 직선보다 작아야 한다. (여기서 $\phi'(0) < 0$)

$$\phi(\alpha) \leq \phi(0)+\mu_1 \alpha \phi'(0) = f(x_k)+ \mu_1 \alpha \nabla f(x_k)p_k$$ $$\phi'(\alpha) = \nabla f(x_k+ \alpha p_k)p_k$$ $$\phi'(0) = \nabla f(x_k)p_k$$

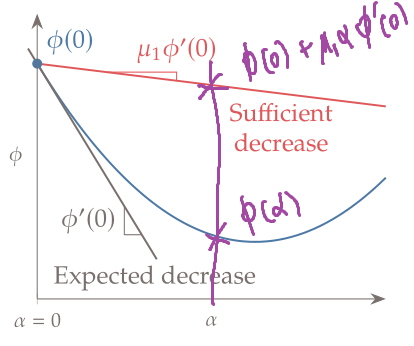
이런 $\alpha$를 찾기 위해서 아래의 알고리즘 절차를 거친다.

1set $\alpha_{\text{init}} > 0$, 
2    $0<\mu_1 <1$, 
3    $0<\rho <1$
4    $\alpha = \alpha_{\text{init}}$
5while $\phi(\alpha) \geq \phi(0)+\mu_1 \alpha \phi'(0)$ do
6    $\alpha = \rho \alpha$
7end while

근데 거의 몇번의 iteration만 거치면 적당한 $\alpha$를 빨리 찾는다. $\phi'(\alpha)$가 너무 steep하면 조건을 만족하는 alpha를 찾기가 힘들다. 이때 strong Wolfe conditions 이라는 것을 적용하여 vertical line처럼 아예 가파르게 되는 지점을 제외시킨다.

$$|\phi'(\alpha)| \leq \mu_2 |\phi'(0)| $$