Penalty method

제약조건이 있는 Constrained optimization을 간단하게 제약조건이 없는 unconstrained optimization으로 변환할 수 있는 방법이다. penalty parameter 설정에 의해서 true optimum에 수렴하지 않을 경우가 있어서 gradient based optimization에서는 더이상 사용되지 않는다. graient free method에서 사용되기도 하고, constrained optimization을 이해하는데 도움이 되기 때문에 살펴보자. 일단 constrained optimization problem의 formulation은 아래와 같다. $$\begin{aligned} \text{minimize} \quad & f(x) & \newline \text{by varying} \quad & x_i & i=1,...,n_x \newline \text{subject to} \quad & g_j(x) \leq 0 & j=1,...,n_g \newline & h_l(x) = 0 & l=1,...,n_h \newline & \underline{x_i} \leq x_i <\overline{x_i} & i=1,...,n_x \end{aligned}$$

여기서 equality constraint $h_l(x)$ 와 inequality constraint $g_j(x)$에 penalty method를 적용하면 objective function은 다음과 같이 변화한다. $$\hat{f}(x;\pi_{\alpha}, \pi_{\beta}) = f(x) + \pi_{\alpha} \sum_{l=1}^{n_h} h_l(x) +\pi_{\beta} \sum_{j=1}^{n_g} \max{[0, g_j(x)]}$$ 이 말은 즉슨, $h_l$이 0이 아니면 $h_l$값과 penalty parameter $\pi_{\alpha}$의 곱이 objective function에 더해져서 objective function 값을 커지한다는 것이다. 또한 $g_j$가 0 보다 크게 되면 max function에서 $g_j(x)$ 값이 반환되어 penalty parameter $\pi_{\beta}$와 곱해져서 objective funciont 값을 크게한다. 따라서 제약조건들을 만족하지 않으면 objective function evaluation에서 penalty를 갖게되어서 minimum solution과 멀어지게 된다.

직관적이고 쉽다. 근데 여기서 문제가 이 penalty parameter를 어떻게 설정하냐 인다. 아래의 그림에서 $\mu$로 표기되어 있는 penalty parameter는 클수록 true optimum을 찾을 가능성이 커지는데 너무 크게되면 argument $x$의 작은 변화에도 아주 민감하게 되어서 또 최적해를 찾기가 어려워 진다.

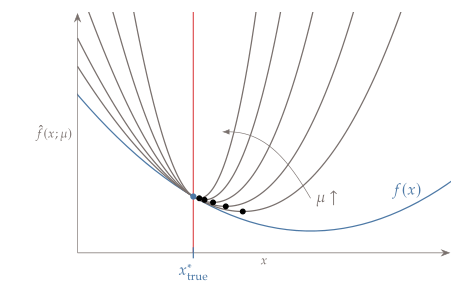
이게, argumented Lagrangian 이랑 비슷하게 생겼는데 다른 점은, penalty parameter에 상응하는 argumented Lagrangian의 Lagrangian은 해를 찾으면서 같이 풀리기 때문에 정할 필요가 없다는 것이다.